 第四章几何图形 章末综合检测含答案Word文档下载推荐.docx
第四章几何图形 章末综合检测含答案Word文档下载推荐.docx
- 文档编号:16857346
- 上传时间:2022-11-26
- 格式:DOCX
- 页数:10
- 大小:129.87KB
第四章几何图形 章末综合检测含答案Word文档下载推荐.docx
《第四章几何图形 章末综合检测含答案Word文档下载推荐.docx》由会员分享,可在线阅读,更多相关《第四章几何图形 章末综合检测含答案Word文档下载推荐.docx(10页珍藏版)》请在冰豆网上搜索。
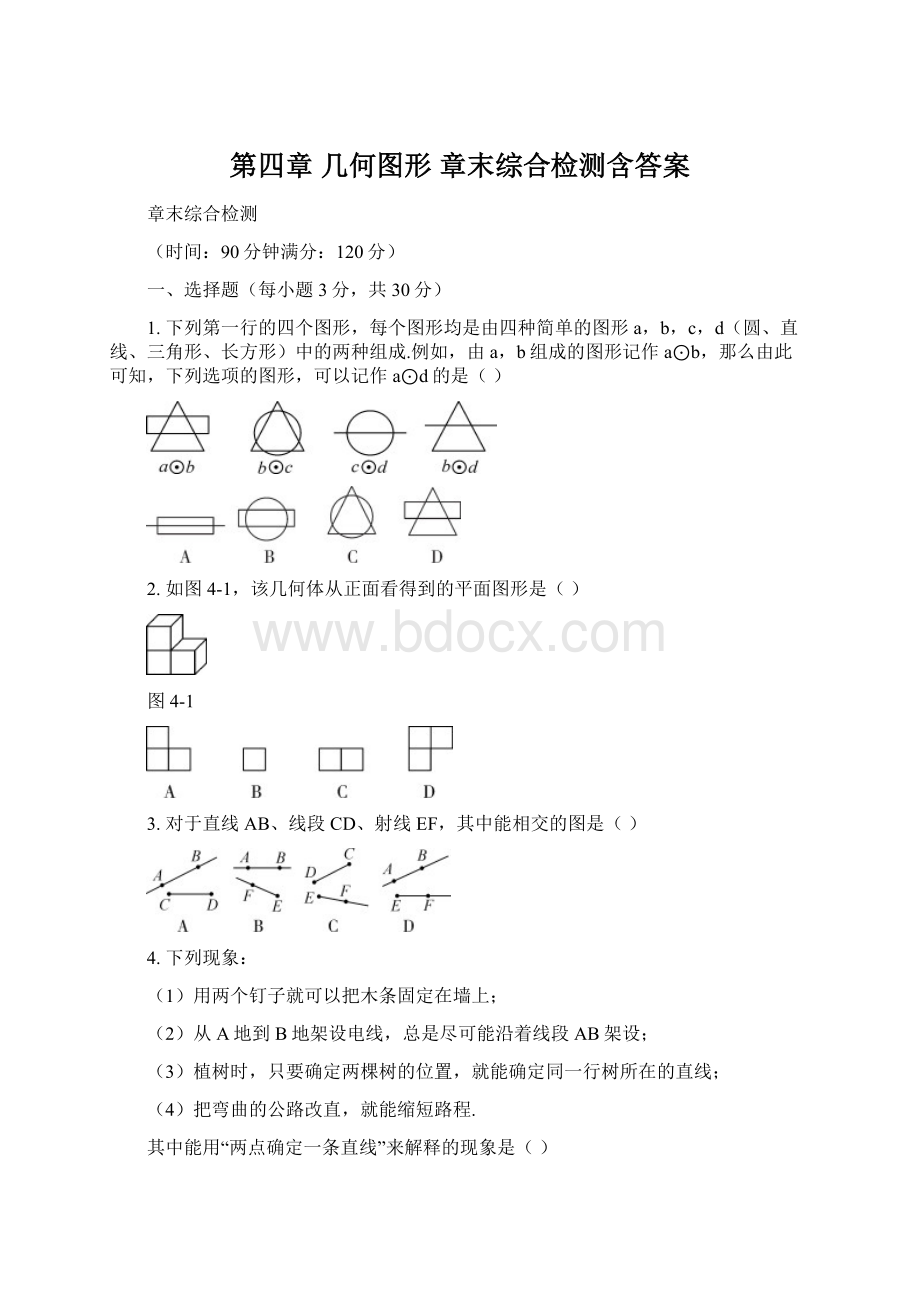
C.点P在线段AB外D.点P在线段AB的延长线上
7.学校、书店、邮局在平面图上的标点分别是A,B,C,书店在学校的正东方向,邮局在学校的南偏西25°
,那么平面图上的∠CAB等于()
A.25°
B.65°
C.115°
D.155°
8.若∠1=40.4°
,∠2=40°
4′,则∠1与∠2的关系是()
A.∠1=∠2B.∠1>∠2
C.∠1<∠2D.以上都不对
图4-3
9.如图4-3,∠AOB=130°
,射线OC是∠AOB内部任意一条射线,OD,OE分别是∠AOC,∠BOC的平分线,下列叙述正确的是()
A.∠DOE的度数不能确定
B.∠AOD+∠BOE=∠EOC+∠COD=∠DOE=65°
C.∠BOE=2∠COD
D.∠AOD=
∠EOC
10.如图4-4,OD⊥AB于点O,OC⊥OE,图中与∠AOC互补的角有()
图4-4
A.1个B.2个C.3个D.4个
二、填空题(每小题4分,共32分)
11.夏天,快速转动的电扇叶片,给我们一个完整的平面的感觉,说明_____.
12.如图4-5,C,D是线段AB上的两点,若AC=4,CD=5,DB=3则图中所有线段长度的和是_____.
图4-5
13.已知∠A=100°
,那么∠A的补角是_____.
14.时钟上3点40分时分针与时针夹角的度数为____.
15.如图4-6,O在直线AB上,∠AOD=90°
,∠COE=90°
,则图中相等的锐角有_____对.
图4-6
16.已知∠AOC和∠BOD都是直角,如果∠AOB=150°
,那么∠COD的度数为_____.
17.如图4-7,一个正方体的表面上分别写着连续的6个整数,且每两个相对面上的两个数的和都相等,则这6个整数的和为_____.
图4-7
18.平面内有四个点A,B,C,D,过其中每两个点画直线可以画出的直线有_____.
三、解答题(共58分)
19.(8分)计算:
(1)22°
18′×
5;
(2)90°
-57°
23′27″.
20.(8分)把图4-8的展开图和它们的立体图形连起来.
图4-8
21.(10分)如图4-9,已知线段a,b,c,用圆规和直尺画图.(不用写作法,保留画图痕迹)
(1)画线段AB,使得AB=a+b-c;
(2)在直线AB外任取一点K,画射线AK和直线BK;
(3)反向延长AK至点P,使AP=KA,画线段PB,比较所画图形中线段PA与BK长度的和与线段AB长度的大小.
图4-9
22.(10分)如图4-10,已知线段AB和CD的公共部分BD=13AB=14CD,线段AB,CD的中点E,F之间的距离是10cm,求线段AB,CD的长度.
图4-10
23.(10分)如图4-11
(1),已知直角三角形两直角边的长分别为3和4,斜边的长为5.
(1)试计算该直角三角形斜边上的高;
(2)按如图4-11
(2),4-11(3),4-11(4)三种情形计算该直角三角形绕某一边旋转得到的立体图形的体积.(结果保留π)
图4-11
24.(12分)如图4-12,O为直线AB上一点,∠AOC=50°
,OD平分∠AOC,∠DOE=90°
.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
图4-12
答案
一、1.A解析:
根据题意,知a代表长方形,d代表直线,所以记作a⊙d的图形是长方形和直线的组合.故选A.
2.A
3.B解析:
A.直线AB与线段CD不能相交,故此选项不符合题意;
B.直线AB与射线EF能相交,故此选项符合题意;
C.射线EF与线段CD不能相交,故此选项不符合题意;
D.直线AB与射线EF不能相交,故此选项不符合题意.故选B.
4.B解析:
(1)用两个钉子就可以把木条固定在墙上,根据是两点确定一条直线;
(2)从A地到B地架设电线,总是尽可能沿着线段AB架设,根据是两点之间,线段最短;
(3)植树时,只要确定两棵树的位置,就能确定同一行树所在的直线,根据是两点确定一条直线;
(4)把弯曲的公路改直,就能缩短路程,根据是两点之间,线段最短.故选B.
5.D解析:
因为C为AB的中点,AB=12,所以AC=BC=
AB=
×
12=6.因为AD∶CB=1∶3,所以AD=2,所以DB=AB-AD=12-2=10.故选D.
6.B解析:
如图D4-1.因为PA+PB=AB,所以点P在线段AB上.故选B.
图D4-1
7.C解析:
如图D4-2.由图可知,∠CAB=∠1+∠2=25°
+90°
=115°
.故选C.
图D4-2
8.B解析:
因为∠1=40.4°
=40°
24′,∠2=40°
4′,所以∠1>∠2.故选B.
9.B解析:
因为OD,OE分别是∠AOC,∠BOC的平分线,所以∠AOD=∠COD,∠EOC=∠BOE.又因为∠AOD+∠BOE+∠EOC+∠COD=∠AOB=130°
,所以∠AOD+∠BOE=∠EOC+∠COD=∠DOE=65°
.故选B.
10.B解析:
根据题意,得
(1)因为∠AOC+∠BOC=180°
,所以∠BOC与∠AOC互补.
(2)因为OD⊥AB,OC⊥OE,所以∠EOD+∠DOC=∠BOC+∠DOC=90°
,所以∠EOD=∠BOC,所以∠AOC+∠EOD=180°
,所以∠EOD与∠AOC互补,所以图中与∠AOC互补的角有2个.故选B.
二、
11.线动成面
12.41解析:
AD=AC+CD=9,AB=AC+CD+DB=12,CB=CD+DB=8,故题图中所有线段长度的和为AC+AD+AB+CD+CB+DB=41.
13.80°
14.130°
解析:
3点40分时分针与时针夹角的度数为30°
4+
=130°
15.2解析:
因为∠AOD=90°
,所以∠AOC+∠COD=90°
.因为∠COE=90°
,所以∠COD+∠DOE=90°
,所以∠AOC=∠DOE.因为∠BOD=180°
-∠AOD=90°
,所以∠DOE+∠BOE=90°
,所以∠BOE=∠COD.故图中相等的锐角有2对.
16.30°
或150°
解析:
如图D4-3
(1),因为∠BOD=90°
,∠AOB=150°
,所以∠AOD=60°
.又因为∠AOC=90°
,所以∠COD=30°
.如图D4-3
(2),因为∠BOD=90°
,∠AOC=90°
,所以∠COD=150°
.综上所述,∠COD的度数为30°
图D4-3
17.51解析:
因为正方体的表面展开图,相对的面一定相隔一个正方形,所以6若不是最小的数,则6与9是相对面.因为6与9相邻,所以6是最小的数,所以这6个整数的和为6+7+8+9+10+11=51.
18.1条、4条或6条解析:
如果A,B,C,D四点在同一直线上,那么只能确定一条直线,如图D4-4
(1);
如果4个点中有3个点(不妨设点A,B,C)在同一直线上,而第4个点,点D不在此直线上,那么可以确定4条直线,如图D4-4
(2);
如果4个点中,任何3个点都不在同一直线上,那么点A分别和点B,C,D确定3条直线,点B分别与点C,D确定2条直线,最后点C,D确定一条直线,这样共确定6条直线,如图D4-4(3).综上所述,过其中每2个点可以画1条、4条或6条直线.
(1)
(2)
(3)
图D4-4
三、19.解:
5=110°
90′=111°
30′.
(2)90°
23′27″=32°
36′33″.
20.解:
如图D4-5.
图D4-5
21.分析:
(1)首先作射线CE在射线CE上截取CD=a,BD=b,再在CB上截取AC=c,则可得出AB=a+b-c;
(2)根据射线和直线的概念过点K即可作出;
(3)根据AP=AK,利用两点之间线段最短即可得出答案.
解:
(1)如图D4-6
(1).
(2)如图D4-6
(2).
图D4-6
(3)如图D4-6(3).
因为AP=KA,所以线段PA与BK长度的和大于线段AB的长度.
22.解:
设BD=xcm,则AB=3xcm,CD=4xcm,AC=6xcm.
因为E,F分别为线段AB,CD的中点,
所以AE=
AB=1.5x(cm),CF=
CD=2x(cm).
所以EF=AC-AE-CF=6x-1.5x-2x=2.5x(cm).
因为EF=10cm,所以2.5x=10,解得x=4.
所以AB=12cm,CD=16cm.
23.解:
(1)三角形的面积为
5h=
3×
4,解得h=12/5.
(2)在图4-11
(2)中,所得立体图形的体积为
π×
32×
4=12π;
在图4-11(3)中,所得立体图形的体积为
42×
3=16π;
在图4-11(4)中,所得立体图形的体积为
(
)2×
5=
π.
24.解:
(1)图中小于平角的角有∠AOD,∠AOC,∠AOE,∠DOC,∠DOE,∠DOB,∠COE,∠COB,∠EOB,共9个.
(2)因为∠AOC=50°
,OD平分∠AOC,
所以∠DOC=1/2∠AOC=25°
,∠BOC=180°
-∠AOC=130°
所以∠BOD=∠DOC+∠BOC=155°
(3)因为∠DOE=90°
,∠DOC=25°
,
所以∠COE=∠DOE-∠DOC=90°
-25°
=65°
又因为∠BOE=∠BOD-∠DOE=155°
-90°
所以∠COE=∠BOE,即OE平分∠BOC.
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 第四章 几何图形 章末综合检测含答案 第四 综合 检测 答案
 冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 转基因粮食的危害资料摘编Word下载.docx
转基因粮食的危害资料摘编Word下载.docx
