 与《三角函数的应用》有关的中考题集锦Word文件下载.docx
与《三角函数的应用》有关的中考题集锦Word文件下载.docx
- 文档编号:18706212
- 上传时间:2022-12-31
- 格式:DOCX
- 页数:32
- 大小:30.84KB
与《三角函数的应用》有关的中考题集锦Word文件下载.docx
《与《三角函数的应用》有关的中考题集锦Word文件下载.docx》由会员分享,可在线阅读,更多相关《与《三角函数的应用》有关的中考题集锦Word文件下载.docx(32页珍藏版)》请在冰豆网上搜索。
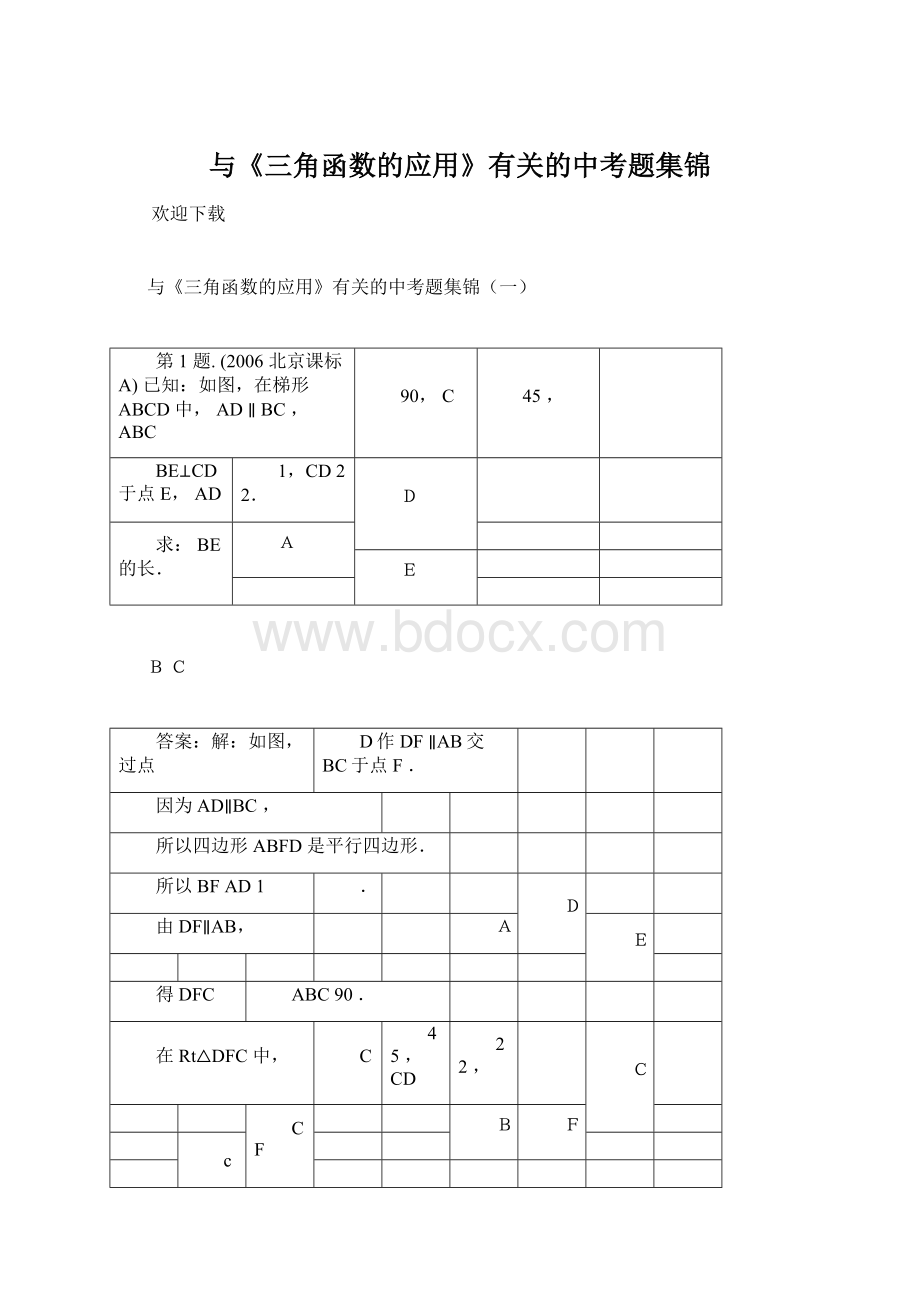
求得BE
32.
5分
2
第2题.(2006梅州课改)梅华中学九年级数学课外学习小组某下午实践活动课时,测量朝西教学楼前的旗杆
AB的高度.如图,当阳光从正西方向照射过来时,旗杆
AB的顶端
A的影子落在教学楼前的坪地
C处,测
得影长
CE
2m,DE
4m,BD
20m,DE与地面的夹角
30
.在同一时刻,测得一根长为
1m的直
立竹竿的影长恰为
4m.根据这些数据求旗杆
AB的高度.(可能用到的数据:
21.414,3
1.732,结果
保留两个有效数字)
A
EC
BD
如图,过点C,E分别作CF⊥AB于点F,EH⊥BD的延长线于H.
在Rt△DEH中,
DE4m,EDH30,
EH
2m,
DH
DE2
EH2
23m
F
AF
1
又
4
CE)
(EF
1(BD
CE)6.4.
AB
EH
AF8.4(m.)
第3题.(2006陕西非课改)如图,小河对岸有一座塔
∠128,∠241,且CD25米.则塔的高度
(可用计算器求,也可用下列参考数据求:
D
BH
AB.分别在点D,C处测得塔尖点A处的仰角为
AB约为米(精确到0.1米).
sin28≈0.4695,sin41≈0.6561
cos28≈0.8829,cos41≈0.7547
21
BC
tan28≈0.5317,tan41≈0.8693)
34.2
第4题.(2006成都课改)如图,某校九年级3班的一个学习小组进行测量小山高度的实践活动.部分同学在
山脚点A测得山腰上一点D的仰角为30,并测得AD的长度为180米;
另一部分同学在山顶点B测得山脚
点A的俯角为45,山腰点D的俯角为60.请你帮助他们计算出小山的高度BC(计算过程和结果都不取
近似值).
HB
45
60
AC
如图,过点D作DEAC于点E,作DFBC于点F,
则有DE∥FC,DF∥EC.
∠DEC90,
四边形DECF是矩形,
DEFC.
∠HBA
∠BAC
∠BAD
∠DAE
453015
又∠ABD∠HBD∠HBA
15,
△ADB是等腰三角形.
ADBD
180(米).
在Rt△AED中,sin∠DAE
sin30
DE
AD
180sin30
180
90(米),
H
B
FC
90米.
在Rt△BDF中,∠BDF
∠HBD
60,
sin∠BDF
sin60
BF
BD
180sin60
3
90
3(米).
903
31(米).
答:
小山的高度
BC为90
1米.
第5题.(2006
荆门大纲)如图,某乡村小学有
A,B两栋教室,B栋教室在A栋教室正南方向
36米处,在A
栋教室西南方向
300
2米的C处有一辆拖拉机以每秒
8米的速度沿北偏东
60的方向CF行驶.若拖拉机的
噪声污染半径为
100
米,试问A,B两栋教室是否受到拖拉机噪声的影响?
若有影响,
影响的时间有多少秒?
(计算过程中
3取1.7,各步计算结果精确到整数
)
北
过点
C作直线AB的垂线,垂足为
D.
设拖拉机行驶路线CF与AD交于点E,
∵AC
300
,2ACD
BH
N
∴CD
AD3002
.300
H
M
在Rt△CDE中,ECD
30,
DE
CtDan30
170
∴BE
30036
过点B作BH⊥CF,垂足为H,则
EBH30.
∵BH
BcEos3
934
80
∵801,0∵B栋教室受到拖拉机噪声影响.
以点B为圆心,100为半径作弧,交CF于M,N两点,
则MN
21002802
260
120.
∵B栋教室受噪声影响的时间为:
1208
15(秒).
作AH⊥CF,H为垂足,则
EAH
30.
又AE
3694130,∴AH
111.
AEcos30130
∵1111,0∴A栋教室不受拖拉机噪声影响.
第6题.(2006泰安非课改)如图,大楼高30m,远处有一塔BC,某人在楼底A
处测得塔顶的仰角为60,爬到楼顶D测得塔顶的仰角为30.则塔高BC为
_________m.
45
第7题.(2006
芜湖课改)一段路基的横断面是直角梯形,如左下图所示,已知原来坡面的坡角
的正弦
值为
0.6,现不改变土石方量,全部利用原有土石方进行坡面改造,使坡度变小,达到如右下图所示的技术
要求.试求出改造后坡面的坡度是多少?
20m
A120m
B1
i?
30m
E
C1
A1
DECDEC1
由左图可知:
BE
DC,BE
30m,sin
0.6,
在Rt△BEC中,
sin
BE,BC
50(m).
0.6
由勾股定理得,EC
40m.
在不改变土石方量,
全部充分利用原有土石方的前提下进行坡面改造,
使坡度变小,则梯形ABCD面积
梯
形A1B1C1D面积.
2030
130
4020
20
120·
EC1,
解得EC1
80(m).
改建后的坡度i
B1E:
EC1
20:
80
1:
4.
第8题.(2006滨州非课改)如图,在距旗杆
4米的A处,用测角仪测得旗杆
顶端C的仰角为60
,已知测角仪
AB的高为1.5米,则旗杆CE的高等于
米.
4
A60
第9题.(2006河南课改)如图,C,D是两个村庄,分别位于一个湖的南、
北两端A和B的正东方向上,且D位于C的北偏东30方向上,CD
6km,
则AB
____________km.
33
东
第10题.
(2006
淮安课改)如图,在离水面高度为
5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的
夹角为
,此人以每秒
0.5米收绳.问:
8秒后船向岸边移动了多少米?
(结果精确到
0.1米)
5米
设
8秒后船移动到点
D,在Rt△ABC中,BC
10,AB53
在
Rt△ACD
中,
6
AD6
511
BDABAD5311≈8.663.325.34≈5.3.
船向岸边移动了5.3米.
第11题.(2006兰州A课改)广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲乙二人分别
站在E,F处,他们看气球的仰角分别是30,45,E点与F点的高度差AB为1米,水平距离CD为5
米,FD的高度为0.5米,请问此气球有多高?
(结果保留到0.1米)
P
EA
FB
CD
设AP
h米
∠PFB
PB
h1
EA
h
在Rt△PFA中,
PA
AEtan30
6tan30
3h
8.2米
63,h
气球的高度为PA
AB
FD
8.2
10.5
9.7米
第12题.(2006常德课改)如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜
坡的坡度i1:
3,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为45,在山坡的坡
顶D处测得铁架顶端A的仰角为60.
(1)求小山的高度;
(4分)
(2)求铁架的高度.(31.73,精确到0.1米)(4分)
(1)如图,过D作DF垂直于坡底的水平线BC于点F.
由已知,斜坡的坡比
i
3,于是tan
DBC
∴坡角
于是在Rt△DFB中,DF
DBsin30
25
即小山高为25
米
(2)设铁架的高AEx.
在Rt△AED中,已知ADE
60,于是
AE
3x
tan60
在Rt△ACB中,已知
ABC
EC
DF
x
又BC
由AC
BC,得x
∴x
25
4,3即.铁3架高
43.3米
第13题.(2006
南通非课改)如图,为了测量某建筑物
AB的高度,在平地上
C处测得建筑物顶端
A的仰
角为30
,沿CB方向前进
12m
到达D处,在D处测得建筑物顶端
A的仰角为
,则建筑物AB的高度等
于(
A.6(31)m
B.6(
1)m
C.12(
D.12(
A
第14题.(2006青岛课改)在一次数学活动课上,老师领令学生测一条南北流向的河宽,如图所示,某学生
在河东岸点A处观测到河对岸水边有一点
C,测得C在A北偏西
31的方向上,沿河岸向北前行
20米到达B
处,测得C在B北偏西45的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.
(参考数值:
tan313,sin311)
52东
过点C作CD⊥AB,垂足为D,
设CD
x米,
在Rt△BCD中,
CBD
∴BD
CD米.
在Rt△ACD中,
DAC
31,
AD
B(D20
米,)x
米,
∵tanDAC
∴3
,∴x
5
20x
30米.
这条河的宽度为
第15题.(2006湖北十堰课改)武当山风景管理区,为提高游客到某景点的安全性,决定将到达该景点的步
行台阶进行改善,把倾角由44减至32,已知原台阶AB的长为5米(BC所在地面为水平面).
(1)改善后的台阶会加长多少?
(精确到0.01米)
(2)改善后的台阶多占多长一段地面?
44o
(1)如图,在Rt△ABC中,
ACABsin445sin44≈3.473.
AC
3.473≈6.554,
sin32
6.554
5≈1.55.
即改善后的台阶会加长
1.55米.
(2)如图,在Rt△ABC中,
ABcos44
5cos44≈3.597.
3.473≈5.558,
tan32
CDBC
5.5583.597≈1.96.
即改善后的台阶多占
1.96米长的一段地面.
学习必备
欢迎下载
第16题.(2006潍坊课改)如图,河边有一条笔直的公路l,公路两侧是平坦的草地.在数学活动课上,老师
要求测量河对岸B点到公路的距离,请你设计一个测量方案.要求:
(1)列出你测量所使用的测量工具;
(2)画出测量的示意图,写出测量的步骤;
(3)用字母表示测得的数据,求出B点到公路的距离.
公路l
(1)测角器、尺子;
(2)测量示意图见右图;
测量步骤:
①在公路上取两点
C,D,使
BCD,
BDC为锐角;
②用测角器测出
BCD
BDC
;
③用尺子测得
④计算求值.
(3)解:
作BACD
CD的长,记为m米;
B到CD的距离为x米,
于点A,在△CAB中,
CAtan
在△DAB中,
ADtan
xx
CA,AD,
tantan
CAADm,
m,
tan
·
tan
xm
第17题.(2006
潍坊课改)已知平行四边形
ABCD,AD
a,AB
b,∠ABC
.点F为线段BC上一
点(端点B,C除外),连结AF,AC,连结DF,并延长DF交AB的延长线于点
E,连结CE.
(1)当F为BC的中点时,求证
△EFC与△ABF的面积相等;
(2)当F为BC上任意一点时,△EFC与△ABF的面积还相等吗?
说明理由.
BFC
(1)证明:
点F为BC的中点,BFCF1BCa,
22
又BF∥AD,
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 三角函数的应用 三角函数 应用 有关 考题 集锦
 冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 铝散热器项目年度预算报告.docx
铝散热器项目年度预算报告.docx
