 第九届华杯赛决赛试题及解答Word格式文档下载.docx
第九届华杯赛决赛试题及解答Word格式文档下载.docx
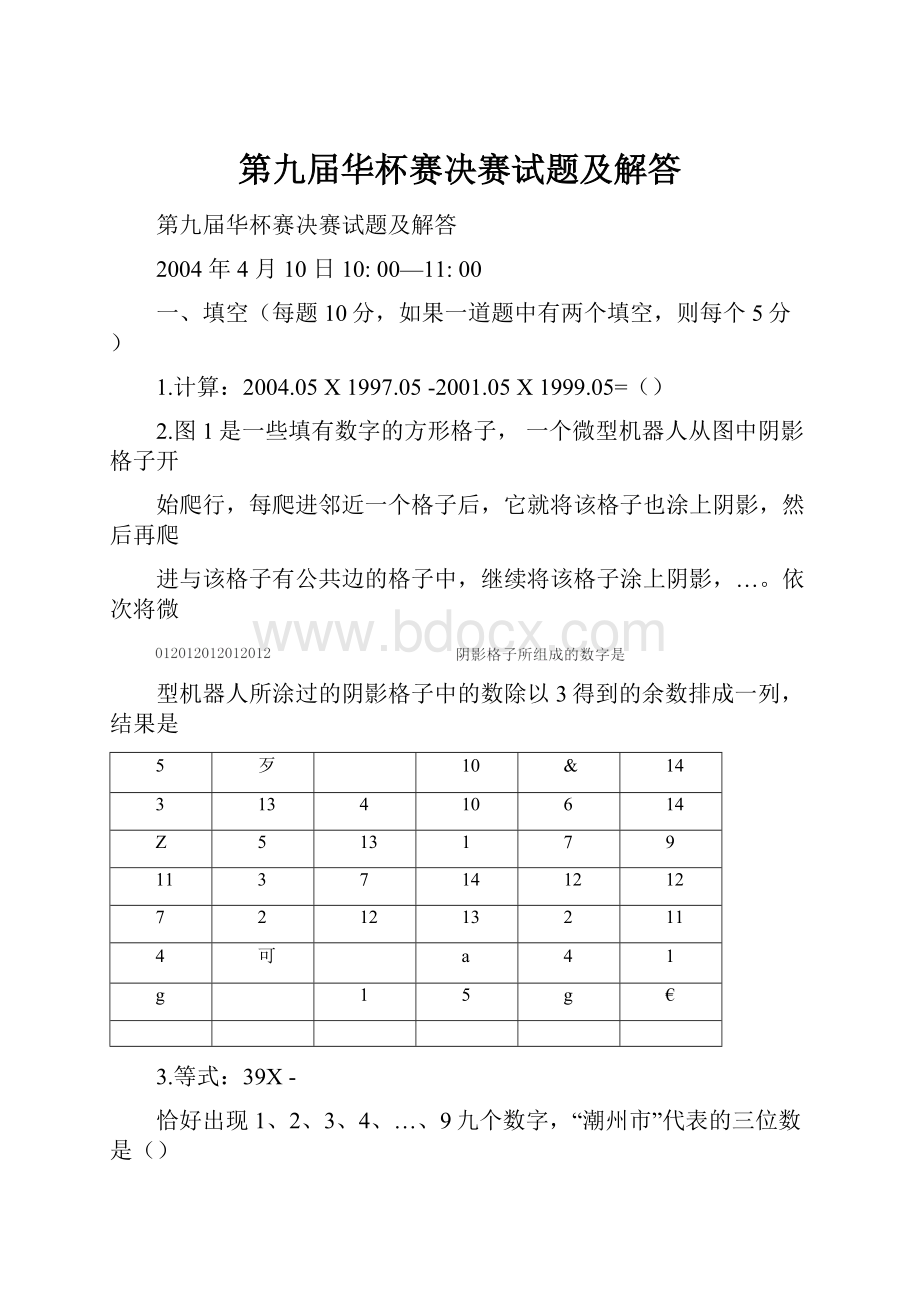
- 文档编号:22209599
- 上传时间:2023-02-03
- 格式:DOCX
- 页数:8
- 大小:88.87KB
第九届华杯赛决赛试题及解答Word格式文档下载.docx
《第九届华杯赛决赛试题及解答Word格式文档下载.docx》由会员分享,可在线阅读,更多相关《第九届华杯赛决赛试题及解答Word格式文档下载.docx(8页珍藏版)》请在冰豆网上搜索。
14
3
13
4
6
Z
1
7
9
11
12
2
可
a
g
€
3.等式:
39X-
恰好出现1、2、3、4、…、9九个数字,“潮州市”代表的三位数是()
4.一个半径为1厘米的圆盘沿着一个半径为4厘米的圆盘外侧做无滑动的滚动,当小圆盘的中心围绕大圆盘中心转动90度后(如图2),小圆
盘运动过程中扫出的面积是()平方厘米。
(匸=3.14)
5.甲、乙、丙三只蚂蚁从AB、C三个不同的洞穴同时出发,分别向洞穴B、C、A爬行,同时到达后,继续向洞穴CAB爬行,然后返回自己出发的洞穴。
如果甲、乙、丙三只蚂蚁爬行的路径相同,爬行的总距离都是7.3米,所用时间分别是6分钟、7分钟和8分钟,蚂蚁乙从洞穴B到达洞穴C时爬行了()米,蚂蚁丙从洞穴C到达洞穴A时爬行了()米。
6.如图3,甲、乙二人分别在A、B两地同时相向而行,于E处相遇后,甲继续向B地行走,乙则休息了14分钟,再继续向A地行走。
甲和乙到达B和A后立即折返,仍在E处相遇,已知甲分钟行走60米,乙每分钟行走80米,则A和B两地相()米。
7.
8.李家和王家共养了521头牛,李家的牛群中有67%是母牛,而王家的牛群中仅有古是母牛,李家和王家各养了多少头牛?
9.一个最简真分数兰,化成小数后,如果从小数点后第一位起连续若干位的数字之和等于2004,求M的值。
10.小丽计划用31元买每支2元、3元、4元三种不同价格的圆珠笔,每种至少买1支。
问她最多能买多少支?
最少能买多少支?
11.在3X3的方格纸上(如图4),用铅笔涂其中的5个方格,要求每横行和每竖行列被涂方格的个数都是奇数,如果两种涂法经过旋转后相同,贝V认为它们是相同类型的涂法,否则是不同类型的涂法。
例如图5
和图6是相同类型的涂法。
回答最多有多少种不同类型的涂法?
说明理由。
Hrrn
rtrl
hhtl
图4图5
12.三个连续正整数,中间一个是完全平方数,将这样的三个连续正整
数的积称为“美妙数”。
问所有的小于2008的“美妙数”的最大公约
数是多少?
13.用455个棱长为1的小正方体粘成一个大的长方体,若拆下沿梭的小正方体,则尚余下371个小正方体,问所粘成的大长方体的棱长各是
多少?
拆下沿棱的小正方体后的多面体(图7是示意图)的表面积是多
少?
一、填空(每题10分,如果一题中有两个填空,则每个5分)
题目
答案
1989.5
728
18.84
2.4;
2.1
1680
二、解答下列各题,写出简要过程(每题10分):
7•解答:
李家和王家各养了300头和221头牛.算术解法:
1李家养牛数的67%是母牛,母牛数应当是整数,67是质数,所以,李
家养牛数应当是100的倍数,可能是500、400、300、200或100头,王家养牛数则可能是21、121、221、321和421头.
丄
2王家的牛群中有匸是母牛,21、121、221、321和421中仅有221能
为13整除,所以,王家养牛数是221头,李家养牛数是300头.
代数解法:
1李家的牛群中有67%是母牛,67是质数,可以设李家养牛头数为100x,
王家的牛群中仅有匸是母牛,13是质数,可以设王家养牛数是13y,列
出方程
100x+13y=521.
②x和y是整数,分别取x=1,2,3,4,5.可以得到x=3,y=13.或者解同余方程(*).
(*)式两边除13,
-4x=1,Mod(13)x=3是(**)式的解,得到y=13.
8解答:
M是3.
■■Q■■
01428571,-=0.28571427
5•■石・"
-=0.7142557,-=1E571428
77
2上面6个最简真分数的循环小数节的数字和都是27,2004被27除的余数是6,仅3/7符合要求.
9.解答:
小丽最多能买14支圆珠笔,小丽最少能买9支圆珠笔.
方法一:
1买圆珠笔总费用是奇数,所以,买3元1支的圆珠笔的数量必须是奇数.
2高价格的笔买的越少,买圆珠笔的总数量就越多,若3元和4元的圆珠笔只各买1支,则小丽能买(31-4-3)-2=12支单价2元的圆珠笔,最多能买12+2=14(支)
3类似,低价格笔买的越少,买圆珠笔总的数量就越少,如果小丽2元
和3元的圆珠笔计划各买1支,余下的钱有26元,能买6支单价4元的笔,尚余2元,可以再买1支2元的圆珠笔.所以,小丽最少能买9支圆珠笔.
方法二:
1设2元、3元、4元的圆珠笔各买x、y、z支,则:
2x+3y+4z=31,(*)
2分析等式(*)的奇偶性,y必须是奇数•因为x,y,z>
1,
3y=31-2x-4z<
25,y<
7.列下表:
y=1
x12108642
z123456
y=3
x13579
z54321
y=5
x246
z321
y=7
x13
z21
从上表,小丽最多能买14支圆珠笔,小丽最少能买9支圆珠笔.
方法三:
①因为x,y,z>
1,所以从(*)式,2x+2y+2z=31-y-2zw31-3=28,得到x+y+zW14.
②取x=12,y=1,z=1满足(*)式,且x+y+z=14.小丽最多能买14支圆
珠笔.
3类似,4x+4y+4z=31+2x+y>
31+3=34,―+三》匸.
取x=2,y=1,z=6满足(*)式,并且,x+y+z=9.小丽最少可以买9支圆
10.解答:
不同类型的涂法有3种,如下图A
说明:
1所涂5个阴影方格分布在3行中,只有一行涂有3个阴影方格.同样,仅有一列涂有3个阴影方格.
2所以,仅有一个方格,它所在的行和列均有3个阴影方格,有这种性质的方格称为“特征阴影方格”.“特征阴影方格”在3X3正方格纸中的位置,就唯一地决定了3X3的方格纸的涂法.“特征阴影方格”
在方格纸的角上(图A左边)、外边中间的方格(图A中间)和中心的方格(图A右边)三个位置确定了只有3种类型的涂法.
11.解答:
60
①任何三个连续正整数,必有一个能为3整除.所以,任何“美妙数”必有因子3.
②若三个连续正整数中间的数是偶数,它又是完全平方数,必定能为4
整除;
若中间的数是奇数,则第一和第三个数是偶数,所以任何“美妙数”必有因子4.
3完全平方数的个位只能是1、4、5、6、9和0,若其个位是5和0,则中间的数必能被5整除,若其个位是1和6,则第一个数必能被5整除,若其个位是4和9,则第三个数必能被5整除.所以,任何“美妙数”必有因子5.
4上述说明“美妙数”都有因子3、4、和5,也就有因子60,即所有的美妙数的最大公约数至少是60.60=3X4X5是一个“美妙数”,美妙数的最大公约至多是60.所有的美妙数的最大公约数既不能大于60,又至少是60,只能是60.
12.解答:
多面体的表面积是358.
1设长方体长宽高分别为x、y、z无仿设x>
z>
y,它们只能取正整数.长方体的体积是455,则有xXyXz=455,分解455=5X7X13,即:
xXyXz=5X7X13
(1)
2沿棱拆下的小正方体有455-371=84个,若认为从“长”边拆下的小正方体为(x-1)个,则从每个“宽”边拆下的小正方体为(y-1)个,而从每个“高”边拆下的小正方体为(z-2)个,应当有下面关系式:
4X(x-1+y-1+z-2)=84,x+y+z=25.
(2)
分析
(1)和
(2),既然x,y,z只取正整数,验证x=13,z=7,y=5是唯一解.
3计算表面积:
如右图B,拆下沿棱的小正方体后的多面体的表面积由两部分
组成:
第一部分是突出在外面的6个平面,总面积是:
2X(11X5+11X3+5X3)=206.
第二部分是24个宽都是1的长条,总面积是:
8X(11+3+5)=152.
拆下沿棱的小正方体后的多面体的表面积和原长方体表面积去
掉8个顶点处的小正方体的三个侧面的面积相同(想像一下为什么).所
以,2X(13X7+13X5+7X5)-3X8=358.
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 第九 杯赛 决赛 试题 解答
 冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 1212中级汽车维修工考试试题三.docx
1212中级汽车维修工考试试题三.docx
