数学单元复习要点.docx

数学单元复习要点.docx

《数学单元复习要点.docx》由会员分享，可在线阅读，更多相关《数学单元复习要点.docx（23页珍藏版）》请在冰豆网上搜索。

数学单元复习要点

三年级下册知识点及例题汇总

单元

知识点

解题方法

例题

第一单元

位置和方向

1、认识东、南、西、北，能根据给定的一个方向辨认其余的方向。

2、会辨认东南、东北、西南、西北四个方向。

方法：

1、选好观察点和目标点。

2、以观察点为中心，画出十字（或者米字）方向，看目标点在观察点的哪一个区域，就可以判断了。

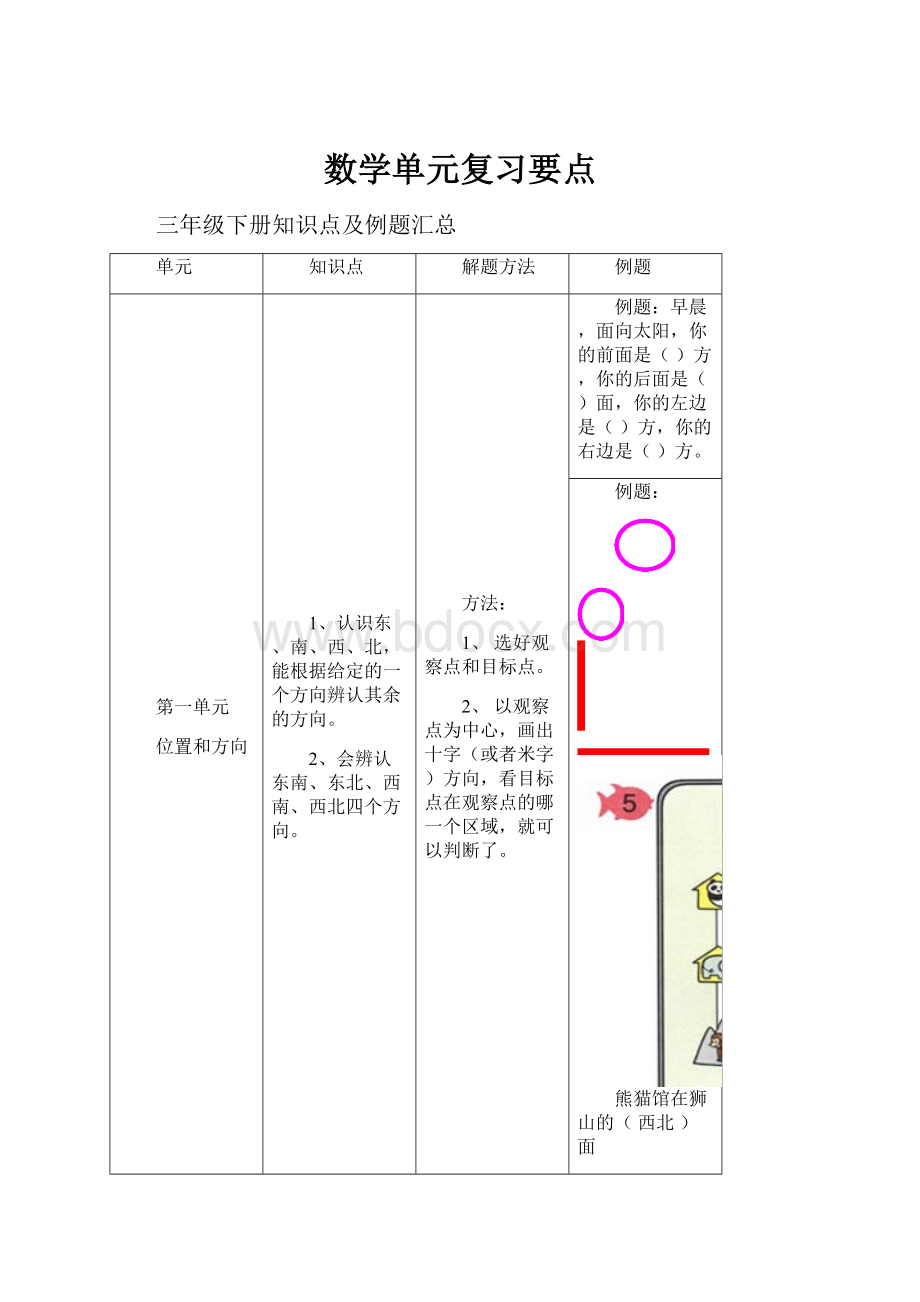
例题：

早晨，面向太阳，你的前面是（）方，你的后面是（）面，你的左边是（）方，你的右边是（）方。

例题：

熊猫馆在狮山的（西北）面

目标点观察点

2、知道地图上的方向。

（地图按“上北下南、左西右东”绘制。

并会看简单的线路图，描述简单的行走路线

注意：

中心点不断在变化

1、描述行走路线：

从火车站出发，向（东南）方走了

（2）站到达（邮局）站；再向（东）走（4）站到达（游泳馆）站；再向（东北）走

（1）站到（少年宫），再向（东）走

（1）站到（电影院）站，再向（东南）方走

（1）站到（动物园）站。

2、小芳从图书馆出发坐了3站，她可能在（）或者（）站下车。

（注意：

起点站不算）

第一单元笔记：

学习东南西北四个方向

1、地图一般按照“上北下南，左西右东”绘制。

有时会在地图的一角画一个向上的箭头表示北方（N）。

2、我们面向东方的时候，后面是西方，左边是北方，右边是南方。

3、东和西相对，南和北相对。

4、描述物体所在位置：

（）在（）的（）方

以观察点为中心，看目的地在观察点的哪一个方向。

5、描述行走路线的方法：

看线路图时，先确定自己的位置（即观察点），再确定目的地与周围事物所处的方向，最后用“先…..再…..”来描述行走的路线。

6、绘制简单的示意图的方法：

先选好观察点，把选好的观察点画在平面图的中心位置，在右上角用向上的箭头标明北方，确定好各物体的方向，在纸上按“上北下南、左西右东”来绘制。

学习东北、东南、西北、西南四个方向

北

7、

西南

西

西北

东南

东

东北

8、东北与西南相对，西北与东南相对。

第二单元除数是一位数的除法

1、一位数除整十、整百、整千数的除法。

（口算）

例题1：

800÷24200÷6

例题2：

210÷2=105（特别注意商末尾没有0，而中间有0）

例题3：

判断商的位数，看被除数的首位是否比除数大，如果比除数大或者等于除数，则商的位数和被除数的位数一样多。

如果被除数的首位比除数小，则商的位数比被除数的位数少1

458÷9（商是两位数）

458÷3（商是三位数）

2、一位数除两位数、三位数、四位数

笔算除法，关键要注意竖式的格式。

尤其是0的位置

例题1：

（商中间有0的除法）

例题2:

例题3：

例题3：

（商末尾有0的除法）易错题

3.除法的验算

用乘法来检验

有余数的除法：

被除数=除数÷商+余数

没有余数的除法：

被除数=除数×商

例题1：

（变形题）

例题1：

如果A÷7=116…..3,那么A=（）×（）+（）=（）

要使余数最大，（）里分别填几？

5（）（）÷9=56……（）

2（）（）÷7=36……（）

4、0除以任何不是0的数都得0

例题：

0÷1=0（0除以0没有意义）

5、除法的估算

1、四舍五入法；

2、根据乘法口诀，把被除数估成比较接近的整百整十数、

6、本单元出现的应用题类型

1、平均分类型：

有48人参加活动，平均分成4个小组，每个小组几人？

48÷4=12（人）

2、包含除类型：

有42个人参加活动，每6个人一组，可以分几组？

42÷6=7（组）

3、估算类：

有124箱苹果，李叔叔三人来运，平均每人大约运多少箱？

124÷3≈40（箱）

4、先除后减类：

小明跳绳一分钟跳124下，小芳五分钟跳了415下，他们俩谁跳得快？

快的比慢的多跳几下？

415÷5=83（下）

124-83=41（下）

5、知道几倍数，求一倍数，用除法计算。

猕猴桃每百克果肉中，含维生素约370毫克，是柑橘的9倍，每百克柑橘中约含维生素多少毫克？

370÷9≈40（毫克）

笔算除法：

步骤：

一商、二乘、三减、四比、五落

除法法则：

1、从被除数的高位起，先用除数试除被除数的前一位数，如果它比除数小，再试除前两位数；

2、除到被除数的哪一位，就把商写在那一位的上面；

3、每求出一位商，余下的数必须比除数小。

第三单元

统计

1、横向条形统计图；

2、起始格与其他格表示不同的单位量。

注意起始格用折线表示。

（统计数据数据较大时，采用起始格表示较大的单位量（省略掉）其他格表示较小单位量的方式。

）

3、求平均数

一组数据的和÷这组数据的个数

即总数量÷总份数=平均数

例：

全班总分÷全班人数=全班的平均分

单元年月日

1、认识年月日，了解它们的关系，知道大月、小月和特殊的2月

例题：

1、一年有（）个月，其中大月是（），小月是（）。

2、平年有（）天，闰年有（）天。

2、学会判断平年和闰年

（易错点）

公历年份是4的倍数的一般是闰年，公历年份是整百数，必须是400的倍数才是闰年

例题：

1、2014年是（）年？

2014÷4=503……2（有余数）

2、1960年是（闰）年。

1960÷4=490

3、2000年是（）年？

2000÷400=5（2000是整百年，必须除以400来判断）

1800年的2月有（28）天？

解：

1800÷400=4……200（1800是整百年，除以400.因为有余数，1800年是平年）

3、24时计时法

12时计时法和24时计时法的转换

12时计时法的前面会有时间限词加以区别。

例：

2时是24时计时法，表示凌晨2时。

下午2时是12时计时法，表示下午2时。

4、开始时刻、经过时间、结束时刻三者关系

1、经过时间=结束时刻—开始时刻

刘老师早上7时到校，下午2：

10分离校，刘老师在校时间有多久？

下午2：

10=14时10分

14时10分—7时=7小时10分

2、开始时刻=结束时刻—经过时间

学校开讲座，开了2小时，10：

30结束，讲座几点开始？

10时30分—2时=8时30分

3、结束时刻=开始时刻+经过时间

一节课是40分钟。

第二节课从9:

30分开始上课，到（）下课？

9时20分+40分=9时60分=10时

路程、时间、速度之间的关系

速度=路程÷经过时间

一辆汽车上午8时从广州出发，下午1时到达汕头，共行驶了400千米，这辆汽车每时行多少千米？

下午1时=13时

13时—8时=5小时

400÷5=80（千米）

路程=速度×经过时间

小明7时从家出发，7:

20分到达学校，他每分钟约走80米，他家到学校大约有多少米？

7时20分—7时=20分

80×20=1600（米）

经过时间=路程÷速度

第五单元

两位数乘两位数

1、笔算

2、乘法估算

22×18≈

3、出现的乘法应用题类型

1、求几个几是多少？

学校有20个班，每个班45人，一共多少人？

2、求一个数的几倍是多少？

学校买来10个篮球，买来乒乓球的数目是篮球的5倍，买了多少个乒乓球？

3、多余条件应用题

一套明信片12张，售价14元，今天卖出56套，一共卖出多少钱？

第六单元

面积

1、定义：

物体的表面或者封闭图形的大小，就是它们的面积。

并根据进率熟练改写单位。

常用的面积单位：

平方厘米—平方分米——平方米——公顷——平方千米

百进百进万进百进

2、了解不同面积单位所代表的实际大小

边长为1厘米的正方形，面积是1平方厘米。

（大约一个手指甲的大小）

边长为1分米的正方形，面积是1平方分米。

（大约数学书封面的一半）

边长为1米的正方形，面积是1平方米。

（课室里4块地砖的大小）

边长为100米的正方形，面积是1公顷（即10000平方米）。

（大约两个穗园校区大小）

边长为1千米的正方形，面积是1平方千米。

（100公顷）

例：

天河公园约71公顷，

香港特别行政区的面积大约1100平方千米，

广州约7000多平方千米，

我国总面积是960万平方千米

长方形正方形面积公式的熟练运用

1、求周长

1、长方形的周长=（长+宽）×2

2、正方形的周长=边长×4

2、周长公式灵活运用

3、知道长方形的周长和宽，求长。

长方形的长=（周长—2×宽）÷2

长方形的长=周长÷2—宽

4、知道长方形的周长和长，求宽。

长方形的宽=（周长—2×长）÷2

长方形的宽=周长÷2—长

5、知道正方形周长，求边长。

正方形的边长=周长÷4

3、面积公式运用

8、长方形的长=面积÷宽

9、长方形的宽=面积÷长

10、知道长方形面积，知道长，求周长。

（两步）

先求宽：

面积÷长=宽

再求周长：

（长+宽）×2=周长

11、知道正方形周长，求正方形面积。

（两步）

先求边长：

周长÷4=边长

再求面积：

边长×边长=面积

12、知道长方形的周长，知道长，求面积。

（两步）

先求宽：

周长÷2—长=宽

再求面积：

长×宽=面积

4、生活中的一些例子

例子：

1、一台压路机，压路的宽度是3米，每分钟行驶40米，压路机10分钟能压多大面积的路？

（注意：

压路机的轨迹是长方形）

先算1分钟压的面积：

3×40=120（平方米）

再算10分钟压的面积：

120×10=1200（平方米）

2、一个教室长8米，宽5米，如果用边长为1米的瓷砖铺地面，需要多少块这样的瓷砖？

（先算教室面积，再算瓷砖面积，最后看教室面积包含几个瓷砖面积）

8×5=40（平方米）

1×1=1（平方1米）

40÷1=40（块）

3、教室前面的墙壁长6米，宽3米。

墙上有一块黑板，面积是3平方米，现在要粉刷这面墙，要分刷的面积是多少平方米？

（实际面积—不需要粉刷的面积）

第七单元

小数的初步认识

1、小数的读写

小数点左边部分按照整数的读法去读，右边的数按照顺序依次去读。

如果是0，也必须读出。

2、小数的含义

1、一位小数表示十分之几，两位小数表示百分之一。

3、小数的大小比较

从整数部分比起，如果相同，再比较十分位，十分位大的那位数就大，如果相同，再比较百分位……

4、简单的小数加、减法

原则：

小数点对齐，相同数位加减。

第八单元

解决问题

乘除法两步应用题

1、连乘类

例题：

（多种方法解决，注意分步算式的单位）

每个方阵有8行，每行有10人，3个方阵一共有多少人？

方法一：

8×10=80（人）80×3=240（人）

方法二：

8×3=24（行）24×10=240（人）

2、乘加、

乘减类

例题：

一张圆桌可以坐3人，有圆桌7张和方桌6张，可同时接待多少客人？

方法一：

3×7=21（人）6×4=24（人）21+24=45（人）

方法二：

3+4=7（人）7×6=42（人）42+3=45（人）

方法三：

6+7=13（张）4×13=52（人）52-7=45（人）

方法四：

6+7=13（张）3×13=39（人）39+6=45（人）

3、连除类

例题：

（多种方法解决，注意分步算式的单位

一共有126本书，分别放在3个书架上，每个书架有6层，平均每层放几本？

4、除减类

一只啄木鸟一天吃645只害虫，一只青蛙8天吃608只害虫，啄木鸟比青蛙每天多吃多少只害虫？

608÷8=76（只）645-76=569（只）

C

B

A

解题步骤：

1、先用字母表示数量关系式：

2、转换成一倍数（1A、1B、或者1C）;3、列出对应算式

6A=2B——》3A=1B——》6÷2=3

9B=3C——》3B=1C——》9÷3=3

6C=?

A6×3×3=54（根）

C

B

A

C

B

A

800克

200克

730克

解题步骤：

1、先用字母表示数量关系式；2、把任意两个算式的左边和右边分别相加；3、和第三个算式对比：

A+B=730A+B+C+B=730+200

C+B=200即A+2B+C=930对比：

得出2B=130

A+C=800A+C=800B=65