一次函数解题策略解析Word文件下载.docx

一次函数解题策略解析Word文件下载.docx

《一次函数解题策略解析Word文件下载.docx》由会员分享，可在线阅读，更多相关《一次函数解题策略解析Word文件下载.docx（6页珍藏版）》请在冰豆网上搜索。

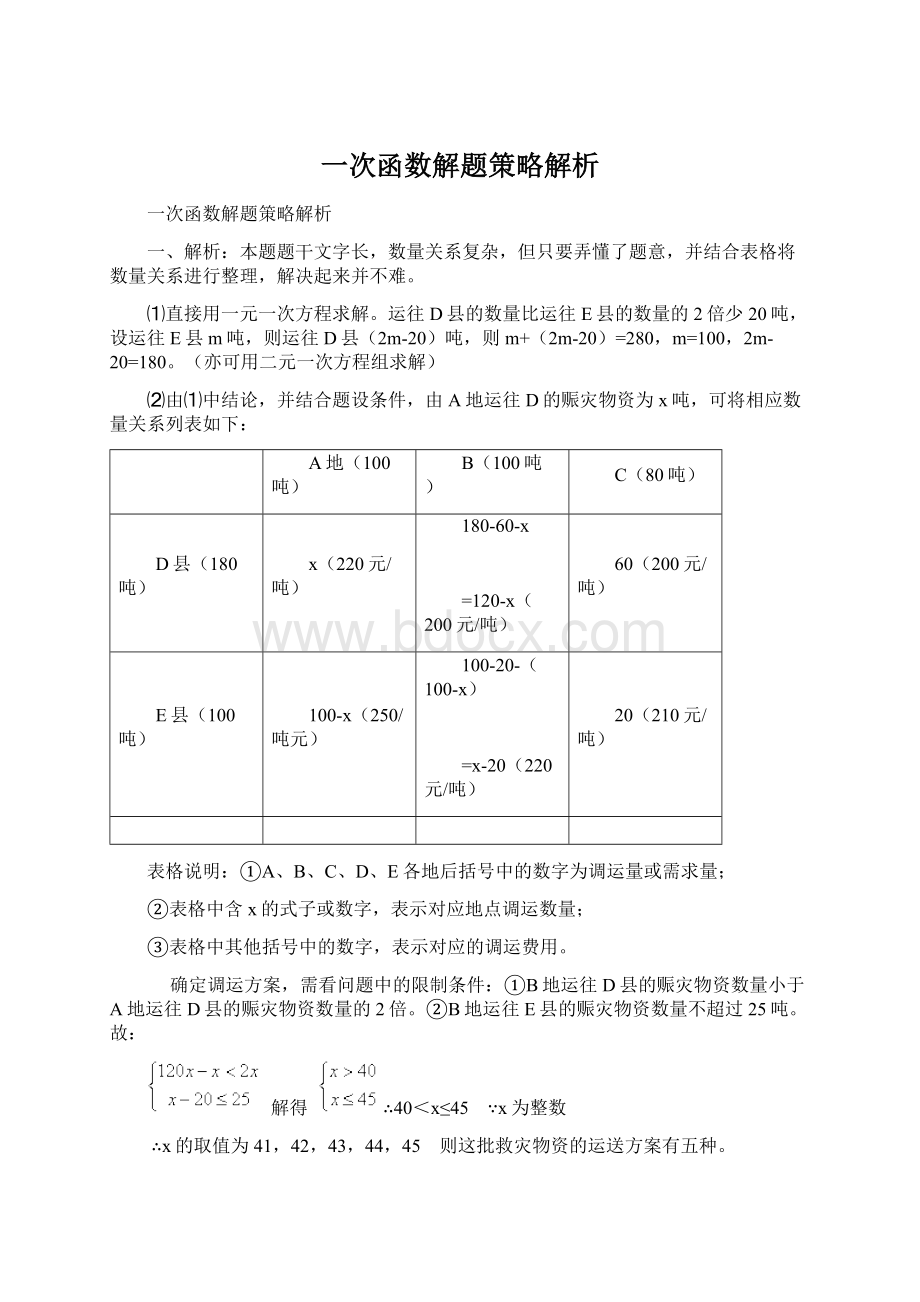
=x-20（220元/吨）

20（210元/吨）

表格说明：

①A、B、C、D、E各地后括号中的数字为调运量或需求量；

②表格中含x的式子或数字，表示对应地点调运数量；

③表格中其他括号中的数字，表示对应的调运费用。

确定调运方案，需看问题中的限制条件：

①B地运往D县的赈灾物资数量小于A地运往D县的赈灾物资数量的2倍。

②B地运往E县的赈灾物资数量不超过25吨。

故：

解得 

∴40＜x≤45 

∵x为整数

∴x的取值为41，42，43，44，45 

则这批救灾物资的运送方案有五种。

方案一：

A县救灾物资运往D县41吨，运往E县59吨；

B县救灾物资运往D县79吨，运往E县21吨。

（其余方案略）

⑶设运送这批赈灾物资的总费用为y，由⑵中表格可知：

y=220x+250（100-x）+200（120-x）+220（x-20）+200×

60+210×

20

=-10x+60800

∵y随x增大而减小，且40＜x≤45，x为整数，

∴当x=41时，y有最大值。

该公司承担运送这批赈灾物资的总费用最多是：

y=-10×

41+60800=60390（元）

求解物资调运问题的一般策略：

⑴用表格设置未知数，同时在表格中标记相关数量；

⑵根据表格中量的关系写函数式；

⑶依题意正确确定自变量的取值范围（一般通过不等式、不等式组确定）；

⑷根据函数式及自变量的取值范围，结合一次函数的性质，按题设要求确定调运方案。

物资调运问题应用广泛，包括调水、调运物资、分配物资等多种类型。

二、解析：

这是一个两种方案的比较问题。

方案比较通常与不等式联系紧密。

比较优惠条件，即通过比较函数值的大小，确定自变量的区间。

⑴中方案一的函数关系式，直接依题意写出：

y1=60x+10000（x≥0）；

方案二的函数关系由图象给出，用待定系数法求解。

当0≤x≤100时，图象为过原点的线段，函数式为正比例函数，可求得y2=100x（0≤x≤100）；

当x＞100时，图象为不过原点的射线，函数式为一次函数，过（100，10000），（150，14000），可求得y2=80x+2000（x＞100）。

⑵购买门票超过100张，比较那种方案最省，了先使y1=y2，求出此时x的值。

然后利用不等式确定方案。

当y1=y2时，60x+10000=80x+2000，解得x=400，即购买400张门票，两种方案费用相同。

当y1＞y2时，解得x＜400，则当100＜x＜400时，选择方案二，总费用最省；

当y1＜y2时，解得x＞400，则当x＞400时，选择方案一，总费用最省。

⑶分两种情况讨论：

（用方程求解）

①甲单位按方案购买的门票少于100张时，设甲买m（m＜100）张，则乙买700-m张。

100m+60（700-m）+10000=58000 

解得m=150（不合题意，舍去）

②甲单位按方案购买的门票少于100张时，设甲买m（m＞100）张，则乙买700-m张

80m+2000+60（700-m）+10000=58000 

解得m=200，700-m=500

求解方案比较问题的一般策略：

⑴在方案比较问题中，不同的方案有不同的函数式。

因此首先需设法求出不同方案各自的函数式。

求函数式时，有图象的，多用待定系数法求；

没有给出图象的，直接依题意进行列式。

⑵方案比较问题通常都与不等式、方程相联系。

比较方案，即比较同一自变量所对应的函数值。

要会将函数问题转化为方程、不等式问题。

⑶方案比较中尤其要注意不同的区间，多对应的大小关系不同。

方案比较问题，在门票、购物、收费、设计等问题中都可涉及。

三、解析：

（1）当时，有．将，代入，得．用8吨水应收水费（元）．

（2）当x＞10时，有．将，代入，得 

∴． 

故当x＞10时，．

（3）因，

所以甲、乙两家上月用水均超过10吨．

设甲、乙两家上月用水分别为吨，吨，

则 

解之，得

故居民甲上月用水16吨，居民乙上月用水12吨．

解分段价格问题的一般策略：

⑴分段函数的特征是：

不同的自变量区间所对应的函数式不同，其函数图象是一个折线。

解决分段函数问题，关键是要与所在的区间相对应。

⑵分段函数中“折点”既是两段函数的分界点，同时又分别在两段函数上。

在求解析式要用好“折点”坐标，同时在分析图象时还要注意“折点”表示的实际意义，“折点”的纵坐标通常是不同区间的最值。

⑶分段函数应用广泛，在收费问题、行程问题及几何动态问题中都有应用。

四、解析：

（1）由图象可知为正比例函数。

S=（t≥0） 

（2）由图象③，M纵坐标为0变为1，则路径为：

M→D→A→N，10秒

（3）当3≤s＜5，即P从A到B时，y=4-s；

当5≤s＜7，即P从B到C时，y=-1；

当7≤s≤8，即P从C到M时，y=s-8．（补全图象略．）

求解几何图形中的动点问题一般策略：

⑴解决几何图形中的动态问题，关键是看动点运动的路径，在不同的路径上，所对应的线段长（高）等不同，由此引起其它变量的变化。

因此根据不同路径以确定自变量的变化区间至关重要。

⑵在不同的区间上求函数表达式，应注意紧密结合几何图形的特征，会将将函数中的变量关系转化为几何图形上的对应线段关系。

⑶动点（动线）问题，引起图形中相关量的变化，多以面积为主。

本题给出的坐标变化相对降低了难度。

但给出的图象较多，涉及到路程与时间、路程与坐标三个变量，共两种函数，在解决问题时，应认真审题。

五、解析：

（1）900；

（2）图中点的实际意义是：

当慢车行驶4h时，慢车和快车相遇．

（3）由图象可知，慢车12h行驶的路程为900km，所以慢车的速度为；

当慢车行驶4h时，慢车和快车相遇，两车行驶的路程之和为900km，所以慢车和快车行驶的速度之和为，所以快车的速度为150km/h．

（4）根据题意，快车行驶900km到达乙地，所以快车行驶到达乙地，此时两车之间的距离为，所以点的坐标为．

设线段所表示的与之间的函数关系式为，把，代入得

解得

所以，线段所表示的与之间的函数关系式为．

自变量的取值范围是．

（5）慢车与第一列快车相遇30分钟后与第二列快车相遇，此时，慢车的行驶时间是4.5h．

把代入，得．此时，慢车与第一列快车之间的距离等于两列快车之间的距离是112.5km，所以两列快车出发的间隔时间是，即第二列快车比第一列快车晚出发0.75h． 

单个函数图象求“式”的一般策略：

⑴单个函数图象，尤其是折线图，在读图过程中一定要正确认识和理解图形上点的坐标的实际意义。

⑵要关注“折点”所表示的意义，用好折点坐标。

⑶用图象求函数式，多用待定系数法，因此要善于寻找图象上点的坐标。

一方面可以从图象上寻找，此外还可以结合题设中的条件寻找。

六、解析：

本题由甲乙两个互相关联但又不同的行程问题构成，函数图象之间彼此相交。

要解决好所求问题，必须深入认识和理解图象中的信息，尤其是已知点坐标的实际意义。

（1）由图象可知：

AB段发生故障。

时间为4.9-3=1.9（小时） 

（2）要求甲组的汽车在排除故障时，距出发点的路程是多少千米。

即要求出B点的纵坐标。

点B在线段BD上，且横坐标为4.9。

只需求出BD所在直线的解析式即可。

C是BD、EF交点，C点的横坐标为6，求出直线EF的解析式，则可得到C点坐标。

从而求出BD解析式，得到B点纵坐标。

设直线EF的解析式为乙=kx+b∵点E（1.25,0）、点F（7.25,480）均在直线EF上

∴ 

∴直线EF的解析式是y乙=80X-100

∵点C在直线EF上，且点C的横坐标为6，

∴点C的纵坐标为80×

6—100=380 

∴点C的坐标是（6，380）

设直线BD的解析式为y甲=mx+n

∵点C（6，380）、点D（7，480）在直线BD上

∴BD的解析式是y甲=100X-220 

∵B点在直线BD上且点B的横坐标为4.9，代入y甲得B（4.9，270）

∴甲组在排除故障时,距出发点的路程是270千米。

（3）符合约定

由图像可知：

甲、乙两组第一次相遇后在B和D相距最远。

在点B处有y乙—y甲=80×

4.9—100—（100×

4.9—220）=22千米＜25千米

在点D有y甲—y乙=100×

7—220—（80×

7—100）=20千米＜25千米

∴按图像所表示的走法符合约定

多个函数图象求式问题的一般策略：

⑴一题中有多个函数图象时，尤其要关注图象交点的坐标。

因其交点坐标同时满足两个图象的关系式。

⑵分析多个函数图象时，还应关注其交点两侧图象的上下位置关系。

图象在上方的函数图象，同一个自变量所对应的函数值大。

由此可比较两个函数图象所表示函数式之间的变化关系。

七、解析：

（1）政府没出台补贴政策前，这种蔬菜的收益额为：

（元）

（2）由题意可设与的函数关系为 

将代入上式

得 

∴ 

∴种植亩数与政府补贴的函数关系为 

同理可得，每亩蔬菜的收益与政府补贴的函数关系为

（3）由题意

∴u

∴当，即政府每亩补贴450元时，全市的总收益额最大，最大为7260000元．

解多个变量及其最值问题的一般策略：

⑴一个问题中涉及多个变量，往往对应着多个函数式。

因此在求解过程中，一定要理清变量之间的对应关系，正确求出不同的函数式。

⑵求函数的最值问题，一次函数主要运用一次函数性质求。

二次函数则可用配方法或公式法求。

⑶对于函数式的求取，则主要是用列式法和待定系数法。