二次函数中三角形面积倍数关系 压轴综合题专题汇编.docx

二次函数中三角形面积倍数关系 压轴综合题专题汇编.docx

《二次函数中三角形面积倍数关系 压轴综合题专题汇编.docx》由会员分享，可在线阅读，更多相关《二次函数中三角形面积倍数关系 压轴综合题专题汇编.docx（19页珍藏版）》请在冰豆网上搜索。

二次函数中三角形面积倍数关系压轴综合题专题汇编

二次函数中三角形面积倍数关系压轴综合题专题汇编

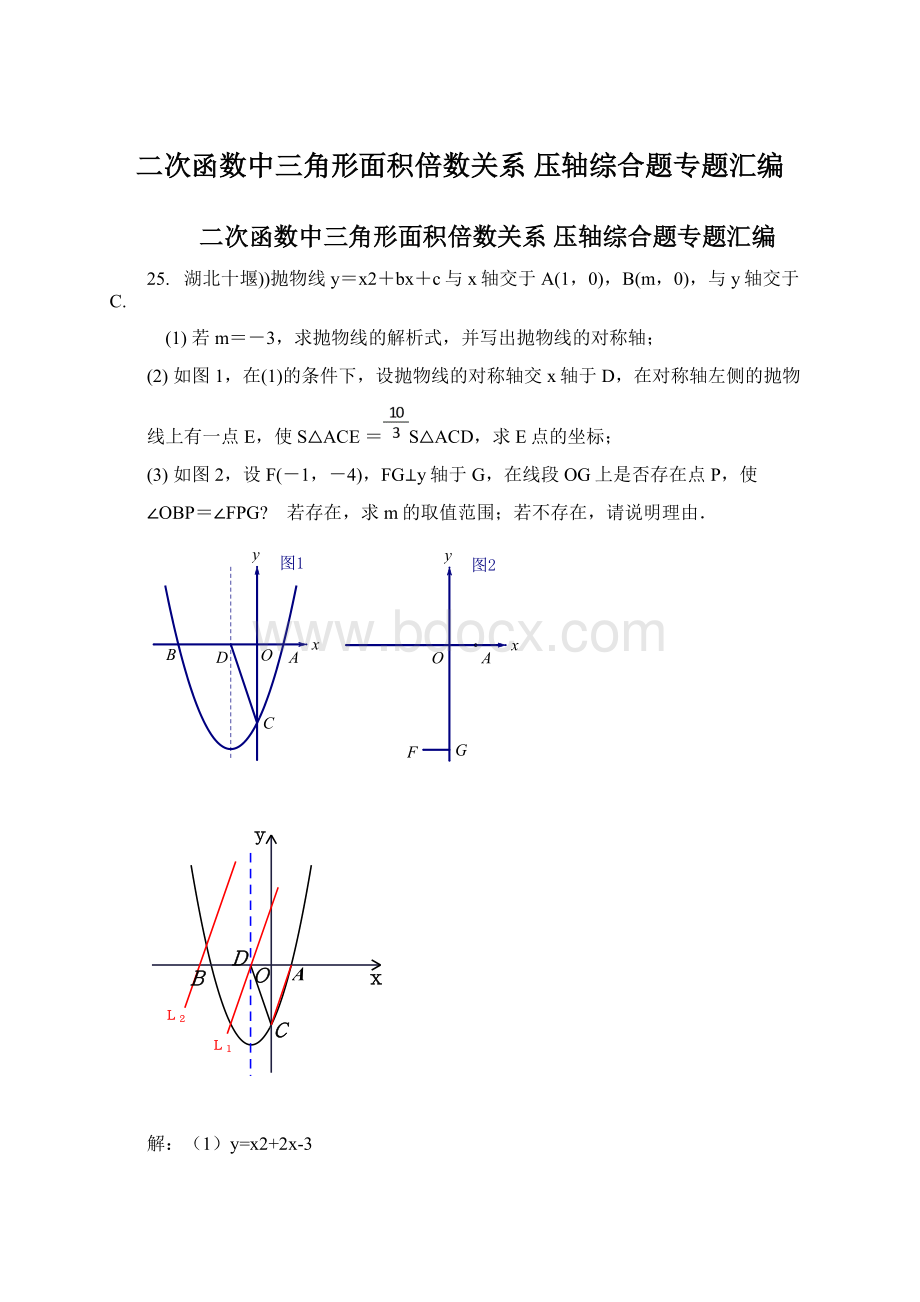
25.湖北十堰））抛物线y＝x2＋bx＋c与x轴交于A（1，0），B（m，0），与y轴交于C.

（1）若m＝－3，求抛物线的解析式，并写出抛物线的对称轴；

（2）如图1，在

（1）的条件下，设抛物线的对称轴交x轴于D，在对称轴左侧的抛物

线上有一点E，使S△ACE＝S△ACD，求E点的坐标；

（3）如图2，设F（－1，－4），FG⊥y轴于G，在线段OG上是否存在点P，使

∠OBP＝∠FPG?

　若存在，求m的取值范围；若不存在，请说明理由．

解：

（1）y=x2+2x-3

（2）∵点A（1，0），C（0，-3）

∴直线AC为y=3x-3

∴过点D（-1，0）且平行于AC的直线L1为：

y=3x+3

∴直线AC向上平移6个单位得到直线L1

∴将直线AC向上平移个单位得到直线L2：

y=3x+17

联立方程组，

y=x2+2x-3

y=3x+17

解得，

x1=-4x1=5

y1=5y1=32（不合题意，舍去）

∴点E坐标为（-4，5）

（3）设点P（0，y）

①当m＜0时，如图所示，易证△POB～△FPG，得

∴

∴m=y2+4y=（y+2）2-4

∵-4＜y＜0

∴-4≤m＜0

②当m＞0时，如图所示，易证△POB～△FPG，得

∴

∴m=-y2-4y=-（y+2）2+4

∵-4＜y＜0

∴0＜m≤4

综上所述，m的取值范围是：

-4≤m≤4，且m≠0.

24．（湖北武汉）已知点A（－1，1）、B（4，6）在抛物线y＝ax2＋bx上

（1）求抛物线的解析式

（2）如图1，点F的坐标为（0，m）（m＞2），直线AF交抛物线于另一点G，过点G作x轴的垂线，垂足为H．设抛物线与x轴的正半轴交于点E，连接FH、AE，求证：

FH∥AE

（3）如图2，直线AB分别交x轴、y轴于C、D两点．点P从点C出发，沿射线CD方向匀速运动，速度为每秒个单位长度；同时点Q从原点O出发，沿x轴正方向匀速运动，速度为每秒1个单位长度．点M是直线PQ与抛物线的一个交点，当运动到t秒时，QM＝2PM，直接写出t的值

【答案】

（1）抛物线的解析式为：

y=x2－x；

（2）证明见解析；（3）；.

（3）进行分类讨论即可得解.

试题解析：

（1）∵点A（－1，1），B（4，6）在抛物线y=ax2+bx上

∴a－b=1，16a+4b=6

解得：

a=，b=－

∴抛物线的解析式为：

y=x2－x

设直线AF的解析式为y=kx+m

∵A（－1,1）在直线AF上，

∴－k+m=1

即：

k=m－1

∴直线AF的解析式可化为：

y=（m－1）x+m

与y=x2－x联立，得（m－1）x+m=x2－x

∴（x+1）（x－2m）=0

∴x=－1或2m

∴点G的横坐标为2m

考点：

二次函数综合题.

24.如图，抛物线与轴交于两点，与轴交于点，其对称轴交抛物线于点，交轴于点，已知.

求抛物线的解析式及点的坐标；

连接为抛物线上一动点，当时，求点的坐标；

平行于轴的直线交抛物线于两点，以线段为对角线作菱形，当点在轴上，且时，求菱形对角线的长.

【考点】HF：

二次函数综合题．

【分析】

（1）由条件可求得B、C坐标，利用待定系数法可求得抛物线解析式，进一步可求得D点坐标；

（2）过F作FG⊥x轴于点G，可设出F点坐标，利用△FAG∽△BDE，由相似三角形的性质可得到关于F点坐标的方程，可求得F点的坐标；

（3）可求得P点坐标，设T为菱形对角线的交点，设出PT的长为n，从而可表示出M点的坐标，代入抛物线解析式可得到n的方程，可求得n的值，从而可求得MN的长．

【解答】解：

（1）∵OB=OC=6，

∴B（6，0），C（0，﹣6），

∴，解得，

∴抛物线解析式为y=x2﹣2x﹣6，

∵y=x2﹣2x﹣6=（x﹣2）2﹣8，

∴点D的坐标为（2，﹣8）；

（2）如图1，过F作FG⊥x轴于点G，

设F（x，x2﹣2x﹣6），则FG=|x2﹣2x﹣6|，

在y=x2﹣2x﹣6中，令y=0可得x2﹣2x﹣6=0，解得x=﹣2或x=6，

∴A（﹣2，0），

∴OA=2，则AG=x+2，

∵B（6，0），D（2，﹣8），

∴BE=6﹣2=4，DE=8，

当∠FAB=∠EDB时，且∠FGA=∠BED，

∴△FAG∽△BDE，

∴=，即==，

当点F在x轴上方时，则有=，解得x=﹣2（舍去）或x=7，此进F点坐标为（7，）；

当点F在x轴上方时，则有=﹣，解得x=﹣2（舍去）或x=5，此进F点坐标为（5，﹣）；

综上可知F点的坐标为（7，）或（5，﹣）；

（3）∵点P在x轴上，

∴由菱形的对称性可知P（2，0），

如图2，当MN在x轴上方时，设T为菱形对角线的交点，

∵PQ=MN，

∴MT=2PT，

设PT=n，则MT=2n，

∴M（2+2n，n），

∵M在抛物线上，

∴n=（2+2n）2﹣2（2+2n）﹣6，解得n=或n=，

∴MN=2MT=4n=+1；

当MN在x轴下方时，同理可设PT=n，则M（2+2n，﹣n），

∴﹣n=（2+2n）2﹣2（2+2n）﹣6，解得n=或n=（舍去），

∴MN=2MT=4n=﹣1；

综上可知菱形对角线MN的长为+1或﹣1．

24．（湖北鄂州）已知，抛物线（a<0）与x轴交于A（3，0）、B两点，与y轴交于点C.抛物线的对称轴是直线x=1，D为抛物线的顶点，点E在y轴C点的上方，且CE=.

（1）求抛物线的解析式及顶点D的坐标；

（2）求证：

直线DE是△ACD外接圆的切线；

（3）在直线AC上方的抛物线上找一点P，使，求点P的坐标；

（4）在坐标轴上找一点M，使以点B、C、M为顶点的三角形与△ACD相似，直接写出点M的坐标.

【考点】二次函数，相似，圆

【解析】

（1）利用对称性求出点B的坐标为（-1,0），再求抛物线的解析式及顶点D的坐标

（2）求证△ACD和△AED为直角三角形，就知道直线DE是△ACD外接圆的切线

（3）找出CD的中点坐标N，再过点N作NP∥AC，就能找到P点

（4）多次利用相似寻找点M

【解答】

（1）∵抛物线的对称轴是直线=1，点A（3,0）

根据抛物线的对称性知点B的坐标为（-1,0）

将（3,0）（-1,0）带入抛物线解析式中得

解得

∴

当=1时，y=4

∴顶点D（1,4）.

（2）当x=0时，y=3

∴点C的坐标为（0,3）

∵A（3,0），D（1,4）

∴

∴

∴△ACD为直角三角形，∠ACD=90°.

∴AD为△ACD外接圆的直径

∵点E在轴C点的上方，且CE=.

∴E（0，）

∵A（3,0），D（1,4）

∴

∴

∴△AED为直角三角形，∠ADE=90°.

∴AD⊥DE

又∵AD为△ACD外接圆的直径

∴DE是△ACD外接圆的切线

（此问中用相似证∠ADE=90°亦可）

（3）

解：

∵A（3,0），D（1,4）,C（0,3）

∴直线AC的解析式y=-x+3

取CD的中点坐标N，则N（，）

过点N作NP∥AC，交抛物线于点,,设直线NP表达式为y=-x+b

把N（，）带入y=-x+b得b=4

∴直线NP表达式为y=-x+4

24（湖北宜昌）．已知抛物线y=ax2+bx+c，其中2a=b＞0＞c，且a+b+c=0．

（1）直接写出关于x的一元二次方程ax2+bx+c=0的一个根；

（2）证明：

抛物线y=ax2+bx+c的顶点A在第三象限；

（3）直线y=x+m与x，y轴分别相交于B，C两点，与抛物线y=ax2+bx+c相交于A，D两点．设抛物线y=ax2+bx+c的对称轴与x轴相交于E．如果在对称轴左侧的抛物线上存在点F，使得△ADF与△BOC相似，并且S△ADF=S△ADE，求此时抛物线的表达式．

【考点】HF：

二次函数综合题．

【分析】

（1）根据a+b+c=0，结合方程确定出方程的一个根即可；

（2）表示出抛物线的对称轴，将2a=b代入，并结合a+b+c=0，表示出c，判断顶点坐标即可；

（3）根据表示出的b与c，求出方程的解确定出抛物线解析式，由直线y=x+m与x，y轴交于B，C两点，表示出OB=OC=|m|，可得出三角形BOC为等腰直角三角形，确定出三角形三角形ADE面积，根据三角形ADF等于三角形ADE面积的一半求出a的值，即可确定出抛物线解析式．

【解答】解：

（1）∵抛物线y=ax2+bx+c，a+b+c=0，

∴关于x的一元二次方程ax2+bx+c=0的一个根为x=1；

（2）证明：

∵2a=b，

∴对称轴x=﹣=﹣1，

把b=2a代入a+b+c=0中得：

c=﹣3a，

∵a＞0，c＜0，

∴△=b2﹣4ac＞0，

∴＜0，

则顶点A（﹣1，）在第三象限；

（3）由b=2a，c=﹣3a，得到x==，

解得：

x1=﹣3，x2=1，

二次函数解析式为y=ax2+2ax﹣3a，

∵直线y=x+m与x，y轴分别相交于点B，C两点，则OB=OC=|m|，

∴△BOC是以∠BOC为直角的等腰直角三角形，即此时直线y=x+m与对称轴x=﹣1的夹角∠BAE=45°，

∵点F在对称轴左侧的抛物线上，则∠DAF＞45°，此时△ADF与△BOC相似，

顶点A只可能对应△BOC的直角顶点O，即△ADF是以A为直角顶点的等腰直角三角形，且对称轴为x=﹣1，

设对称轴x=﹣1与OF交于点G，

∵直线y=x+m过顶点A（﹣1，﹣4a），

∴m=1﹣4a，

∴直线解析式为y=x+1﹣4a，

联立得：

，

解得：

或，

这里（﹣1，﹣4a）为顶点A，（﹣1，﹣4a）为点D坐标，

点D到对称轴x=﹣1的距离为﹣1﹣（﹣1）=，AE=|﹣4a|=4a，

∴S△ADE=××4a=2，即它的面积为定值，

这时等腰直角△ADF的面积为1，

∴底边DF=2，

而x=﹣1是它的对称轴，此时D、C重合且在y轴上，由﹣1=0，

解得：

a=1，此时抛物线解析式为y=x2+2x﹣3．

27（江苏盐城）．如图，在平面直角坐标系中，直线y=x+2与x轴交于点A，与y轴交于点C，抛物线y=x2+bx+c经过A、C两点，与x轴的另一交点为点B．

（1）求抛物线的函数表达式；

（2）点D为直线AC上方抛物线上一动点；

①连接BC、CD，设直线BD交线段AC于点E，△CDE的面积为S1，△BCE的面积为S2，求的最大值；

②过点D作DF⊥AC，垂足为点F，连接CD，是否存在点D，使得△CDF中的某个角恰好等于∠BAC的2倍？

若存在，求点D的横坐标；若不存在，请说明理由．

【考点】HF：

二次函数综合题．

【分析】

（1）根据题意得到A（﹣4，0），C（0，2）代入y=﹣x2+bx+c，于是得到结论；

（2）①如图，令y=0，解方程得到x1=﹣4，x2=1，求得B（1，0），过D作DM⊥x轴于M，过B作BN⊥x轴交于AC于N，根据相似三角形的性质即可得到结论；

②根据勾股定理的逆定理得到△ABC是以∠ACB为直角的直角三角形，取AB的中点P，求得P（﹣，0），得到PA=PC=PB=，过作x轴的平行线交y轴于R，交AC的延线于G，情况一：

如图，∠DCF=2∠BAC=∠DGC+∠CDG，情况二，∠FDC=2∠BAC，解直角三角形即可得到结论．

【解答】解：

（1）根据题意得A（﹣4，0），C（0，2），

∵抛物线y=﹣x2+bx+c经过A、C两点，

∴，

∴，

∴y=﹣x2﹣x+2；

（2）①如图，令y=0，

∴﹣x2﹣x+2=0，

∴x1=﹣4，x2=1