小高奥数几何三角形五大模型及例题解析.docx

小高奥数几何三角形五大模型及例题解析.docx

《小高奥数几何三角形五大模型及例题解析.docx》由会员分享，可在线阅读，更多相关《小高奥数几何三角形五大模型及例题解析.docx（18页珍藏版）》请在冰豆网上搜索。

小高奥数几何三角形五大模型及例题解析

三角形五大模型

专题知识点概述】

本讲复习以前所学过的有关平面几何方面的知识，旨在提高学生对该部分知识的综合运用能力。

重点模型重温

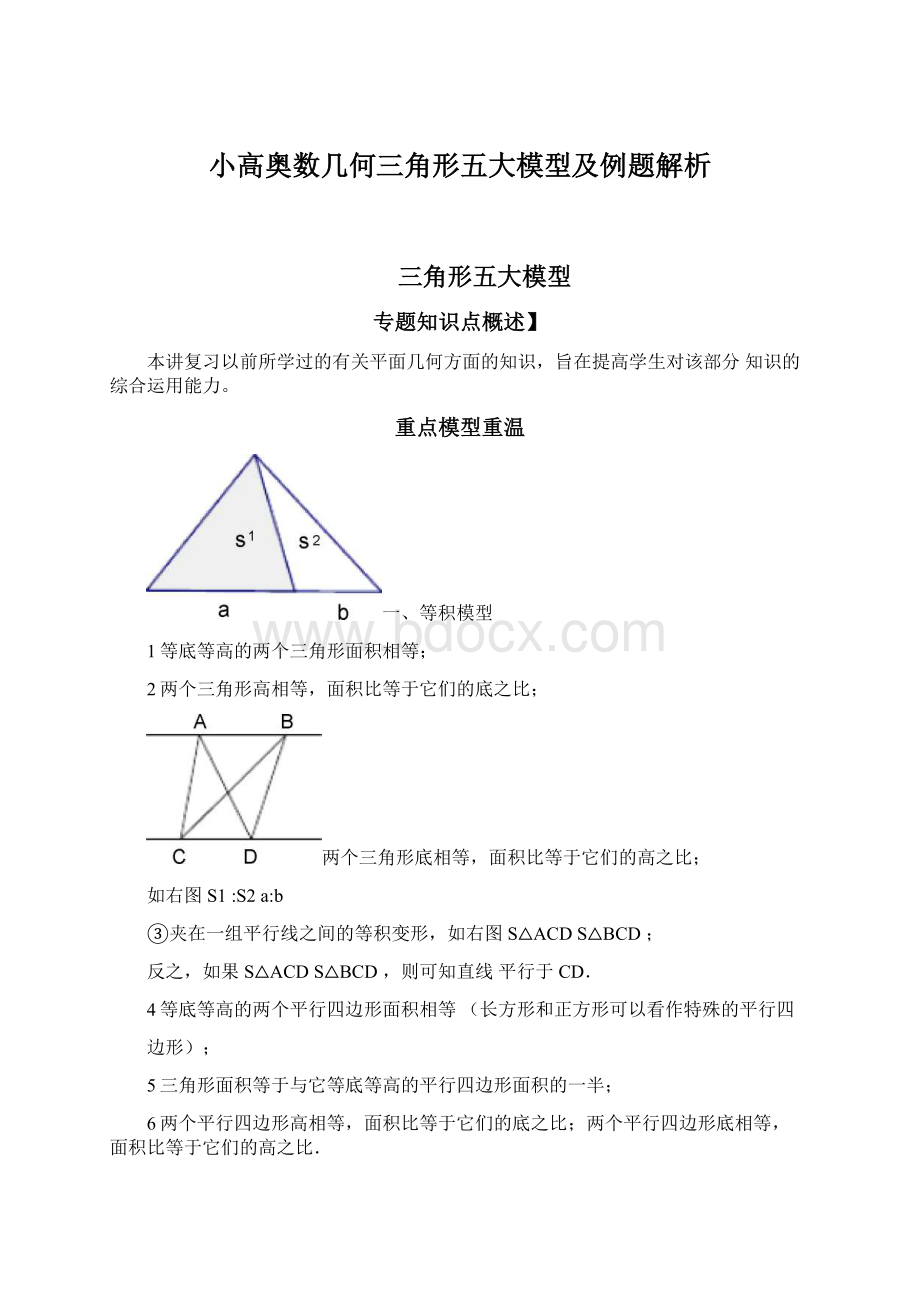
一、等积模型

1等底等高的两个三角形面积相等；

2两个三角形高相等，面积比等于它们的底之比；

两个三角形底相等，面积比等于它们的高之比；

如右图S1:

S2a:

b

③夹在一组平行线之间的等积变形，如右图S△ACDS△BCD；

反之，如果S△ACDS△BCD，则可知直线平行于CD．

4等底等高的两个平行四边形面积相等（长方形和正方形可以看作特殊的平行四

边形）；

5三角形面积等于与它等底等高的平行四边形面积的一半；

6两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比．

、等分点结论（“鸟头定理）”

211

如图，三角形AED占三角形ABC面积的32×14=16

三、任意四边形中的比例关系（“蝴蝶定理）”

①S1︰S2=S4︰S3或者S1×S3=S2×S4

②②AO︰OC=（S1+S2）︰（S4+S3）

梯形中比例关系（“梯形蝴蝶定理）”

①S1︰S3=a2︰b2

②S1︰S3︰S2︰S4=a2︰b2︰ab︰ab;

3S的对应份数为（a+b）2

模型四：

相似三角形性质

如何判断相似

（1）相似的基本概念：

两个三角形对应边城比例，对应角相等。

（2）判断相似的方法：

①两个三角形若有两个角对应相等则这两个三角形相似；

三角形相似。

②S1︰S2=a2︰A2

模型五：

燕尾定理

重点难点解析】

1.模型一与其他知识混杂的各种复杂变形

2.在纷繁复杂的图形中如何辨识“鸟头”

习题精讲】

【例1】（难度等级※）

如图，长方形ABCD的面积是56平方厘米，点E、F、G分别是长方形ABCD边上的中点，H为AD边上的任意一点，求阴影部分的面积.

例2】（难度等级※）

例4】（难度等级※※※）

如图，在面积为1的三角形ABC中，DC=3BD,F是AD的中点，延长CF交AB边于E,求三角

形AEF和三角形CDF的面积之和。

例5】（难度等级※※）

如右图BE=BC，CD=AC，那么三角形AED的面积是三角形ABC面积的几分之几？

【例6】（难度等级※）

如图所示，四边形ABCD与AEGF都是平行四边形，请你证明它们的面积相等．

例7】（难度等级※）

【例8】（难度等级※※）

如图，正方形ABCD的边长为4厘米，EF和BC平行，ECH的面积是7平方厘米，求EG的

长。

例10】（难度等级※※）

如图已知四边形ABCD和CEFG都是正方形，且正方形ABCD的边长为10厘米，那么图中阴影三角形BFD的面积为多少平方厘米?

【例11】（难度等级※※）

如图，一个长方形被切成8块，其中三块的面积分别为12，23，32，则图中阴影部分的面积为?

例12】（难度等级※※※）

如图，平行四边形ABCD周长为75厘米，以BC为底时高是14厘米；以CD为底时高是16

厘米。

求平行四边形ABCD的面积。

例13】（难度等级※※※）

如右图，正方形ABCD的边长为6厘米，△ABE、△ADF与四边形AECF的面积彼此相等，求

三角形AEF的面积.

【例14】（难度等级※※※）

如图，三角形ABC被分成了甲（阴影部分）、乙两部分，BD=DC=，4BE=3，AE=6，甲部分面积是乙部分面积的几分之几？

例15】（难度等级※）

某公园的外轮廓是四边形ABCD，被对角线AC、BD分成四个部分，△AOB面积为1平方

千米，△BOC面积为2平方千米，△COD的面积为3平方千米，公园陆地的面积是6.92

【例16】（难度等级※※）

图中是一个正方形，其中所标数值的单位是厘米．问：

阴影部分的面积是多少平方厘米

作业】

1.如图，三角形ABC中，DC2BD，CE3AE，三角形ADE的面积是20平方厘米，三角形ABC的面积是多少？

的面积。

2.如右图所示，在长方形内画出一些直线，已知边上有三块面积分别是13，35，49．那么图中阴影部分的面积是多少？

ABCD，BE=AB，CF=2CB，GD=3DC，

HA=4AD，平行四边形ABCD的面积是2，求平行四

1

5.如图，在△ABC中，延长BD=AB，CE=BC，F是AC的中点，

2

若△ABC的面积是2，则△DEF的面积是多少？

【例1】（难度等级※）

如图，长方形ABCD的面积是56平方厘米，点E、F、G分别是长方形ABCD边上的中点，H为AD边上的任意一点，求阴影部分的面积.

分析与解】如右图，连接BH、HC，由E、F、G分别为AB、BC、CD三边的中点有AE=EB、BF=FC、CG=CD.

因此S1=S2，S3=S4，S5=S6,而阴影部分面积=S2+S3+S6，空白部分面积=S1+S4+S5.所以阴影部分面积与空白部分面积相等，均为长方形的一半，即阴影部分面积为28.

面积

之和为1CFCD1CFAB.所以阴影部分面积为

1BF

2

2

1BCAB

1346（平方厘米）

AB

1

CFAB

2

2

2

2

例3】（难度等级※）

如图，在三角形ABC中，BC=8厘米，AD=6厘米，E、F分别为AB和AC的中点，那么三角形EBF的面积是多少平方厘米？

【分析与解】

首先，

SABC

1BCAD24平方厘米，而

2

F是AC中点，

1

所以SABF2SABC.又E是AB中点，所以

11

SEBF2SABF4SABC6平方厘米

例4】（难度等级※※※）

如图，在面积为

1的三角形ABC中，DC=3BD,F是AD的中点，延长

CF交AB边于E,求三角

形AEF和三角形CDF的面积之和。

【分析与解】

连接DE,于是三角形AEF的面积=三角形EFD的面积，所求被转化为三角形EDC的面积。

因为F是AD中点，所以三角形AEC的面积和三角形EDC的面积相等，设SBDE为1份,

C

则SAEC=SEDC为3份因此SABC一共7份，

13

每份面积为所以SEDC占3份为。

77

例5】（难度等级※※）

如右图BE=BC，CD=AC，那么三角形AED的面积是三角形ABC面积的几分之几？

【分析与解】

图中，三角形AEC与三角形ABC的高相等，而BE=BC，于是

EC=BC，SAEC

SABC

1又由于三角形AED与三角形AEC的高相等，而CD=AC,于是

4

3SAED3

AD=AC,AED

4SAEC4

332

所以，三角形AED的面积=×三角形AEC的面积=××三角形

443

C

ABC的面积

=1×三角形ABC的面积

2

【例6】（难度等级※）

如图所示，四边形ABCD与AEGF都是平行四边形，请你证明它们的面积相等．

【分析与解】

连接BE

所以SABCDSAEGF

例7】（难度等级※）

由ABCD和CEFG都是正方形有BDCDCF45

所以BDCF.

由平行线间距离相等知三角形BDF和三角形BDC同底等高

例11】（难度等级※※）

如图，一个长方形被切成8块，其中三块的面积分别为12，23，32，则图中阴影部分的面积为?

【分析与解】

如右图，已知a+b+x=23+a+32+12+b所以x=23+32+12

x=67.

例12】（难度等级※※※）

如图，平行四边形ABCD周长为75厘米，以BC为底时高是14厘米；以CD为底时高是16

厘米。

求平行四边形ABCD的面积。

【分析与解】

BC×14=CD×16，BC：

CD=16：

14，

757516

BC+CD=，BC=×=20

221614

ABCD面积=14×20=280（平方厘米）

【例13】（难度等级※※※）

如右图，正方形ABCD的边长为6厘米，△ABE、△ADF与四边形AECF的面积彼此相等，求

三角形AEF的面积.

【分析与解】

因为△ABE、△ADF与四边形AECF的面积彼此相等，所以四边

形AECF的面积与△ABE、△ADF的面积都等于正方形面积的三

分之一，也就是：

1

S四边形AECFS△ABES△ADF36612

在△ABE中，因为AB＝6.所以BE＝4，同理DF＝4，因此CE＝CF＝2，

∴△ECF的面积为2×2÷2＝2．

所以S△AEFS四边形AECFS△ECF=122=10（平方厘米）

例14】（难度等级※※※）

例15】（难度等级※）

所以SAOD1321.5平方千米，故公园总面积为

1321.57.5平方千米，人工湖面积为7.56.920.58平方千米

【例16】（难度等级※※）图中是一个正方形，其中所标数值的单位是厘米．问：

阴影部分的面积是多少平方厘米?

分析与解】如下图所示，为了方便所叙，将某些点标上字母，并连接BG．

设△AEG的面积为x，显然△EBG、△BFG、△FCG的面积均为x，则△ABF的面积为3x，

1100

SABF2010100即x，那么正方形内空白部分的面积为23

400

4x.

3

所以原题中阴影部分面积为2020400800（平方厘米）．

33

作业】

1.

厘米，三角形ABC的面积是多少？

如图，三角形ABC中，DC2BD，CE3AE，三角形ADE的面积是20平方

答案】120

2.如右图所示，在长方形内画出一些直线，已知边上有三块面积分别是13，35，49．那

么图中阴影部分的面积是多少？

【答案】97

3.右图是由大、小两个正方形组成的，小正方形的边长是的面积。

【答案】8

4.如图，平行四边形ABCD，BE=AB，CF=2CB，GD=3DC，HA=4AD，平行四边形ABCD的面积是2，求平行四边形ABCD与四边形EFGH的面积比.

答案】1：

17

6.如图，在△ABC中，延长则△DEF的面积是多少？

【答案】3.5

1

BD=AB，CE=BC，F是AC的中点，若△ABC的面积是2，

2

E