 高二数学双曲线复习专题及考试题型.doc
高二数学双曲线复习专题及考试题型.doc
- 文档编号:2142205
- 上传时间:2022-10-27
- 格式:DOC
- 页数:5
- 大小:209.04KB
高二数学双曲线复习专题及考试题型.doc
《高二数学双曲线复习专题及考试题型.doc》由会员分享,可在线阅读,更多相关《高二数学双曲线复习专题及考试题型.doc(5页珍藏版)》请在冰豆网上搜索。
双曲线---专项复习
【1、基本知识点】
双曲线的第一定义:
双曲线的第二定义:
注意点:
(1)双曲线定义中,“距离的差”一定要加绝对值,否则只表示双曲线的一支。
(2)定义中的小于这一限制条件
标准方程:
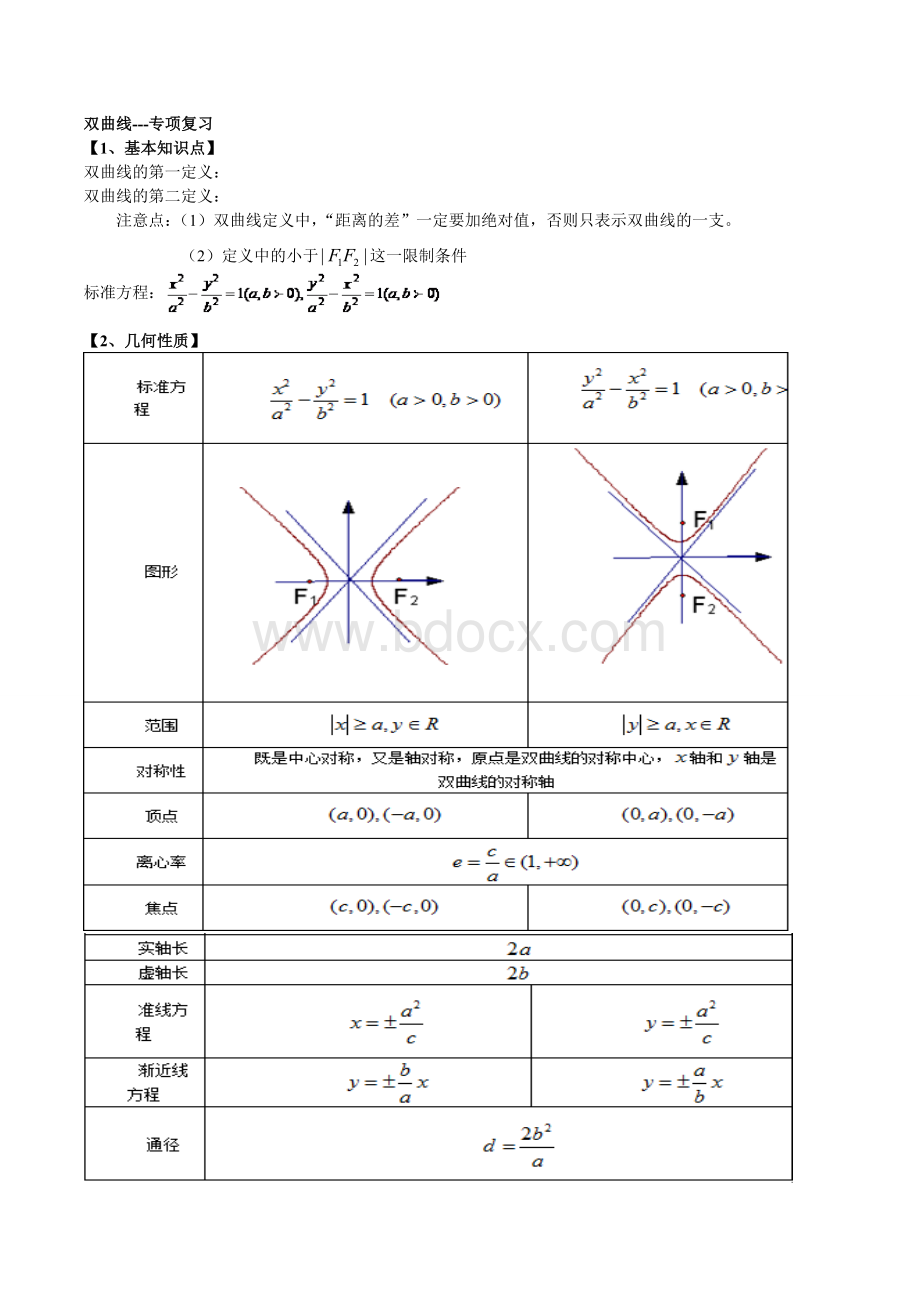
【2、几何性质】
【3、弦长公式】
1、若直线与圆锥曲线相交于两点A、B,且分别为A、B的横坐标,
则,,
若分别为A、B的纵坐标,则。
2、通径的定义:
过焦点且垂直于实轴的直线与双曲线相交于A、B两点,则弦长。
3、若弦AB所在直线方程设为,则=。
4、特别地,焦点弦的弦长的计算是将焦点弦转化为两条焦半径之和后,利用第二定义求解
【4、常见双曲线题型】
题型一 双曲线定义的应用
1、如图所示,在△ABC中,已知|AB|=4,且三内角A、B、C满足2sinA+sinC=2sinB,建立适当的坐标系,求顶点C的轨迹方程.
解 :
如图所示,以AB边所在的直线为x轴,AB的垂直平分线为y轴,建立直角坐标系,
则A(2,0)、B(2,0).由正弦定理得sinA=,sinB=,sinC=.
∵2sinA+sinC=2sinB,∴2a+c=2b,即ba=.从而有|CA||CB|=|AB|=2<|AB|.
由双曲线的定义知,点C的轨迹为双曲线的右支.∵a=,c=2,∴b2=c2a2=6.
所以顶点C的轨迹方程为(x>).
【反思感悟】 使用双曲线的定义时易漏掉“差的绝对值”,即||PF1||PF2||=2a,而|PF1|-|PF2|=2a表示一支.
2、P是双曲线-=1上一点,F1、F2是双曲线的两个焦点,且|PF1|=9,求|PF2|的值.
解 在双曲线-=1中,a=4,b=2.
故c=6.由P是双曲线上一点,
得||PF1|-|PF2||=8.
∴|PF2|=1或|PF2|=17.
又|PF2|≥c-a=2,得|PF2|=17.
3、已知双曲线的左右焦点分别是、,若双曲线上一点P使得,求的面积。
题型二 由方程研究几何性质
4、求双曲线9y2-16x2=144的实半轴长、虚半轴长、焦点坐标、离心率和渐近线方程.
解 把方程9y2-16x2=144化为标准方程-=1.由此可知,实半轴长a=4,
虚半轴长b=3;c===5,焦点坐标是(0,-5),(0,5);
离心率e==;渐近线方程为y=±x.
【反思感悟】 求双曲线的几何性质可先将双曲线方程化为标准形式-=1(或-=1),再根据它确定a,b的值,进而求出c.
5.若方程+=1表示双曲线,则实数k的取值范围是( )
A.k<-2,或2
解析 由题意知:
(|k|-2)(5-k)<0,即
或解得:
k>5,或-2 题型三 由几何性质求双曲线的标准方程 6、设双曲线与椭圆+=1有相同的焦点,且与椭圆相交,一个交点A的纵坐标为4,求此双曲线的标准方程. 解 方法一 设双曲线的标准方程为-=1(a>0,b>0),由题意知c2=36-27=9,c=3. 又点A的纵坐标为4,则横坐标为±,于是有 解得 所以双曲线的标准方程为-=1. 方法二 将点A的纵坐标代入椭圆方程得A(±,4),又两焦点分别为F1(0,3),F2(0,-3).所以 2a=|- | =4, 即a=2,b2=c2-a2=9-4=5, 所以双曲线的标准方程为-=1. 方法三 若考虑到双曲线与椭圆有相同的焦点,则可设双曲线为+=1(27<λ<36),再将点A(±,4)代入求λ,进而求方程,不过这种解题方法有一定的技巧性. 7、求实轴长为4且过点A(2,-5)的双曲线的标准方程 解析 由题意知2a=4,a2=20,若双曲线焦点在x轴上,则可设方程为-=1, 代入点A(2,-5),得: -=1,即=,矛盾. 因此设双曲线的方程为-+=1.代入A(2,-5),得: =-1+=,∴b2=16. 8.双曲线与椭圆+=1有相同的焦点,它的一条渐近线为y=x,则双曲线方程为( ) A.x2-y2=96B.y2-x2=160C.x2-y2=80D.y2-x2=24 答案 D 解析 由题意知双曲线的焦点为(0,±4),即c2=48,又因一条渐近线方程为y=x. 所以=1.即a=b,∴48=2a2,a2=b2=24.故选D. 9、(重庆高考)已知双曲线-=1(a>0,b>0)的一条渐近线为y=kx(k>0),离心率e=k,则双曲线方程为( ) A.-=1B.-=1C.-=1D.-=1 解析 双曲线的渐近线方程可表示为y=±x,由已知可得k=.又离心率e==k,所以k=. 即=,故a=2b.答案 C 10、已知双曲线-=1(a>0,b>0)的两条渐近线方程为y=±x,若顶点到渐近线的距离为1,则双曲线方程为____________. 解析 双曲线顶点为(a,0),渐近线为x+y=0,∴1==,∴a=2. 又=,∴b=,∴双曲线方程为-y2=1. 题型四 求双曲线的离心率 11、已知双曲线的渐近线方程为y=±x,则双曲线的离心率为________; 12、设双曲线-=1(b>a>0)的半焦距为c,直线l过(a,0)、(0,b)两点.已知原点到直线l的距离为c,则双曲线的离心率为________. 解析 (1)当焦点在x轴上时,其渐近线方程为y=±x,依题意,=,e2===1+=, ∴e=;当焦点在y轴上时,其渐近线方程为y=±x, 依题意=,e2===1+=,∴e=. (2)直线l的方程为+=1,即bx+ay-ab=0.于是有=c,即ab=c2. 两边平方得16a2b2=3c4,∴16a2(c2-a2)=3c4.即3c4-16a2c2+16a4=0,∴3e4-16e2+16=0. 解得e2=4,或e2=,∵b>a>0,∴>1,∴e2==1+>2,故e2=4,∴e=2. 答案 (1)或 (2)2 13、(全国Ⅱ高考)设a>1,则双曲线-=1的离心率e的取值范围是( ) A.(,2)B.(,)C.(2,5)D.(2,) 解析 ∵双曲线方程为-=1,∴c=. ∴e===.又∵a>1,∴0<<1.∴1<+1<2. ∴1<2<4.∴ 题型五 直线与双曲线 14、直线l在双曲线-=1上截得的弦长为4,其斜率为2,求直线l在y轴上的截距m. 解 设直线l的方程为y=2x+m, 由得10x2+12mx+3(m2+2)=0. 设直线l与双曲线交于A(x1,y1),B(x2,y2)两点,由韦达定理,得x1+x2=-m,x1x2=(m2+2). 又y1=2x1+m,y2=2x2+m,∴y1-y2=2(x1-x2),∴|AB|2=(x1-x2)2+(y1-y2)2=5(x1-x2)2 =5[(x1+x2)2-4x1x2]=5[m2-4×(m2+2)]. ∵|AB|=4,∴m2-6(m2+2)=16.∴3m2=70,m=±.∴直线l在y轴上的截距为±. 题型六 直线与双曲线的位置关系 16、已知双曲线x2-y2=4,直线l: y=k(x-1),试讨论实数k的取值范围. (1)直线l与双曲线有两个公共点; (2)直线l与双曲线有且只有一个公共点;(3)直线l与双曲线没有公共点. 解 由消去y, 得(1-k2)x2+2k2x-k2-4=0(*) (1)当1-k2=0,即k=±1,直线l与双曲线渐近线平行,方程化为2x=5,故此方程(*)只有一个实数解,即直线与双曲线相交,且只有一个公共点. (2)当1-k2≠0,即k≠±1时, Δ=(2k2)2-4(1-k2)(-k2-4)=4(4-3k2) ①即-<k<,且k≠±1时,方程(*)有两个不同的实数解,即直线与双曲线有两个公共点. ②即k=±时,方程(*)有两个相同的实数解,即直线与双曲线有两重合的公共点. ③即k<-或k>时,方程(*)无实数解,即直线与双曲线无公共点. 综上所述,当-<k<-1或-1<k<1或1<k<时,直线与双曲线有两个公共点. 当k=±1或k=±时,直线与双曲线有且只有一个公共点. 当k<-或k>时,直线与双曲线没有公共点. 【反思感悟】 讨论直线和双曲线的公共点的个数问题,常常归结为讨论含参数的一元二次方程在特定区间内是否存在实根或讨论实根的个数问题,但要注意转化的等价性. 17、过双曲线x2-=1的右焦点F作直线l交双曲线于A、B两点,若|AB|=4,这样的直线有( ) A.1条 B.2条C.3条D.4条 解析 右焦点坐标为(,0),把x=代入双曲线方程得: y=±2,即当直线过右焦点.垂直于x轴时,l与双曲线交的弦长|AB|=4,当l与x轴重合时,|AB|=2.由数形结合知,还存在两条直线,使得|AB|=4,故选C. 知识点七、焦点三角形问题 18、F1、F2为双曲线-y2=-1的两个焦点,点P在双曲线上,且∠F1PF2=90°,则△F1PF2的面积是( ) A.2B.4C.8D.16 解析 方程变形为y2-=1,由题意由①式两边平方得: 20-2|PF1||PF2|=4, ∴|PF1||PF2|=8,S△F1PF2=|PF1|·|PF2|=×8=4.
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 数学 双曲线 复习 专题 考试 题型
 冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 保育笔记.doc
保育笔记.doc
 幼儿园日常安全检查记录表.xls
幼儿园日常安全检查记录表.xls
