高考数学立体几何大题训练.doc

高考数学立体几何大题训练.doc

《高考数学立体几何大题训练.doc》由会员分享，可在线阅读，更多相关《高考数学立体几何大题训练.doc（38页珍藏版）》请在冰豆网上搜索。

高考数学立体几何大题训练

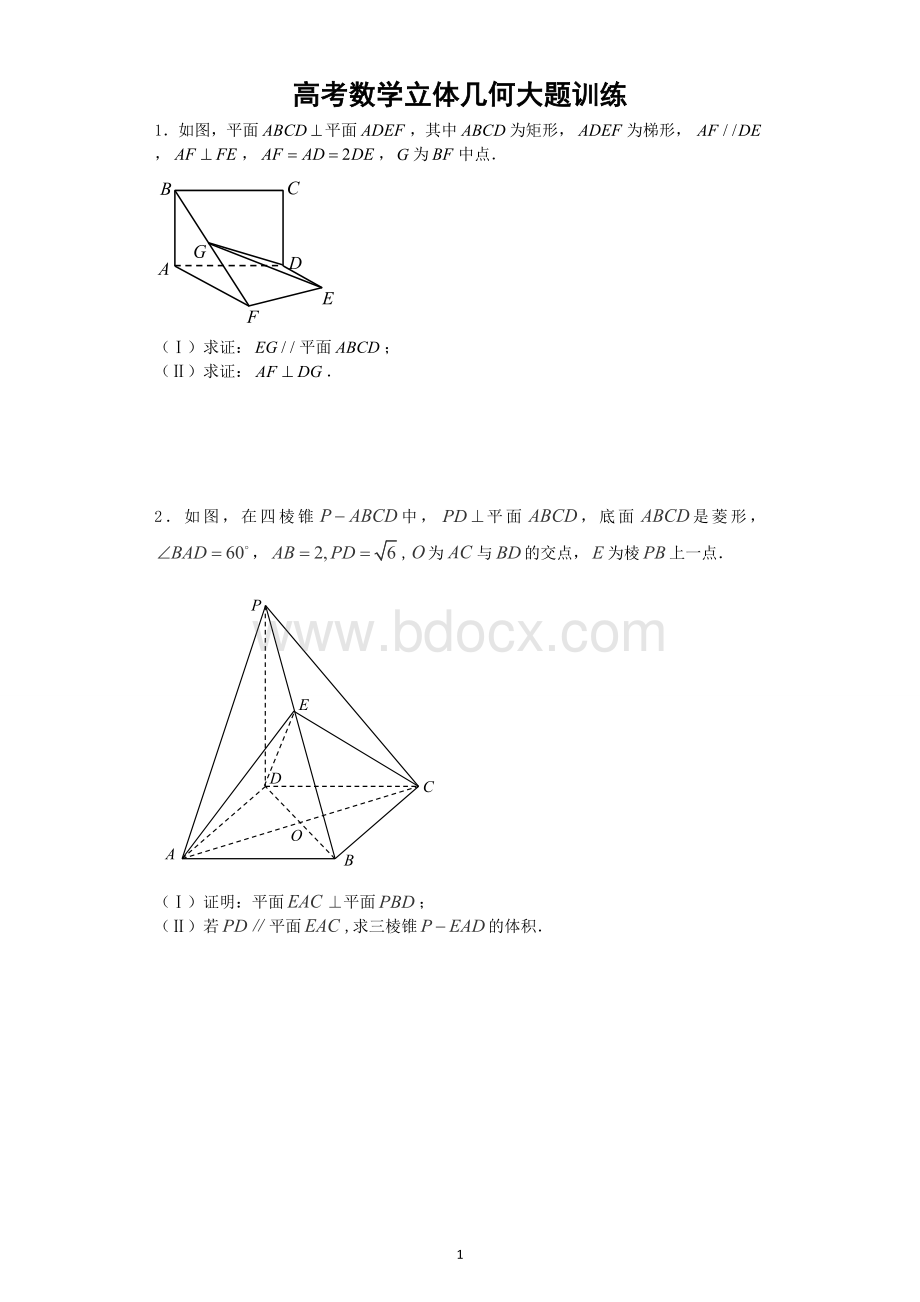
1．如图，平面平面，其中为矩形，为梯形，，，，为中点．

（Ⅰ）求证：

平面；

（Ⅱ）求证：

．

2．如图，在四棱锥中，平面，底面是菱形，，,为与的交点，为棱上一点．

P

A

B

C

D

E

O

（Ⅰ）证明：

平面⊥平面；

（Ⅱ）若平面,求三棱锥的体积．

3．如图，已知四边形ABCD是正方形，平面ABCD，CD=PD=2EA,PD//EA，F，G，H分别为PB，BE，PC的中点.

（Ⅰ）求证：

GH//平面PDAE；

（Ⅱ）求证：

平面平面PCD.

4．如图，在矩形中，点为边上的点，点为边的中点，,现将沿边折至位置，且平面平面.

（Ⅰ）求证：

平面平面；

（Ⅱ）求四棱锥的体积．

5．如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1.

（Ⅰ）求证：

AF⊥平面CBF；

（Ⅱ）设FC的中点为M，求证：

OM∥平面DAF；

（Ⅲ）设平面CBF将几何体EFABCD分成的两个锥体的体积分别为，求.

6．如图所示，在正方体中，分别是棱的中点．

E

A

B

C

D

B1

A1

D1

C1

F

（Ⅰ）证明：

平面平面；

（Ⅱ）证明：

//平面；

（Ⅲ）若正方体棱长为1，求四面体的体积.

7．如图，四棱锥中，是正三角形，四边形是矩形，且平面平面，，．

（Ⅰ）若点是的中点，求证：

平面；

（Ⅱ）若点在线段上，且，当三棱锥的体积为时，求实数的值．

8．如图，三棱柱中，侧棱垂直底面，，，D是棱的中点.

（1）证明：

平面；

（2）若，求三棱锥的体积.

9．已知平行四边形，，，，为的中点，把三角形沿折起至位置，使得，是线段的中点.

（1）求证：

；

（2）求证：

面面；

（3）求四棱锥的体积.

10．如图,已知边长为2的的菱形与菱形全等，且,平面平面，点为的中点.

（Ⅰ）求证：

平面；

（Ⅱ）求证：

；

（Ⅲ）求三棱锥的体积.

11．如图,三棱柱中,,,平面平面,与相交于点.

C

C1

B1

A

A1

B

D

（Ⅰ）求证:

平面；

（Ⅱ）求二面角的余弦值.

12．如图，已知四边形ABCD为正方形，平面，∥，且

（1）求证：

平面；

（2）求二面角的余弦值.

13．如图，在四棱锥中，底面是正方形，侧面底面，，点是的中点，点在边上移动．

（Ⅰ）若为中点，求证：

//平面；

（Ⅱ）求证：

；

（Ⅲ）若，二面角的余弦值等于，试判断点在边上的位置，并说明理由.

14．已知几何体的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形．

（1）求此几何体的体积的大小；

（2）求异面直线DE与AB所成角的余弦值；

（3）求二面角A-ED-B的正弦值．

15．如图，在直三棱柱中，平面侧面，且

（1）求证：

；

（2）若直线与平面所成的角为，求锐二面角的大小.

16．如图所示，正方形与矩形所在平面互相垂直，，点为的中点.

（1）求证：

∥平面；

（2）求证：

；

（3）在线段上是否存在点，使二面角的大小为？

若存在，求出的长；若不存在，请说明理由.

17．如图，在三棱柱中，平面，，为棱上的动点，.

⑴当为的中点，求直线与平面所成角的正弦值；

⑵当的值为多少时，二面角的大小是45.

18．如图，在四棱锥中，平面平面.

（1）证明：

平面;

（2）求二面角的大小

19．如图，正方形与梯形所在的平面互相垂直，，∥，，，为的中点．

（1）求证：

∥平面；

（2）求证：

平面平面；

（3）求平面与平面所成锐二面角的余弦值.

20．在如图所示的几何体中，四边形为平行四边形，，平面，，，，.

（1）若是线段的中点，求证：

平面；

（2）若，求二面角的余弦值.

9

参考答案

1．（Ⅰ）详见解析;（Ⅱ）详见解析

【解析】

试题分析：

证明：

（Ⅰ）取的中点，连接，可得，又因为，

所以，四边形为平行四边形，所以，在根据线面平行的判定定理，即可证明结果．（Ⅱ）取的中点，连接、，可得，因为平面平面，，所以平面，，所以，因为，

所以四边形为平行四边形，，又，所以，根据线面垂直的判定定理，即可证明结果．

试题解析：

证明：

（Ⅰ）取的中点，连接

因为分别是,的中点，

所以，2分

又因为，

所以，四边形为平行四边形

所以4分

因为平面，平面

所以平面5分

（Ⅱ）取的中点，连接、

因为分别是,的中点，

所以，7分

因为平面平面，

所以平面，

所以9分

因为，

所以四边形为平行四边形，

又，所以11分

因为

所以平面

所以12分

考点：

1．线面平行的判定定理；2．线面垂直的判定定理．

2．（Ⅰ）证明见解析；（Ⅱ）．

【解析】

试题分析：

（Ⅰ）要证面面垂直需证线面垂直，根据题意，需证平面，因为底面为菱形对角线互相垂直，又因为平面，所以平面得证；（Ⅱ）根据线面平行的性质定理可知：

平行平面与平面的交线,同时为中点,所以为中点，所以三棱锥的体积等于三棱锥即为三棱锥体积的一半,进而求得三棱锥的体积．

试题解析：

（Ⅰ）平面,平面,．

四边形是菱形,,又,平面．

而平面,平面⊥平面．6分

（Ⅱ）平面,平面平面,,

是中点,是中点．

P

A

B

C

D

E

O

H

取中点,连结,四边形是菱形,,

又,平面,

．9分

．12分

考点：

1．面面平行的判定定理;2．线面平行的性质定理;3．三棱锥的体积公式．

3．

（1）证明详见解析；

（2）证明详见解析.

【解析】

试题分析：

本题主要考查线线平行、线面平行、线线垂直、线面垂直等基础知识，考查学生的分析问题解决问题的能力、空间想象能力、逻辑思维能力、计算能力.第一问，取PD、EA中点，利用中位线得，，而，∴，∴说明是平行四边形，∴，∴利用线面平行的判定平面；第二问，先利用线面垂直的性质得，再利用线面垂直的判定得平面，即平面，最后利用面面垂直的判定得平面平面.

试题解析：

（1）分别取的中点的中点连结.

因为分别为的中点，所以.

因为，所以,

故四边形是平行四边形.所以.4分

又因为平面，平面，

所以平面.6分

（2）证明：

因为平面，平面，所以.

因为所以平面.

因为分别为的中点，所以

所以平面

因为平面，所以平面平面.12分

考点：

线线平行、线面平行、线线垂直、线面垂直.

4．（Ⅰ）见解析（Ⅱ）

【解析】

试题分析：

对于第一问要证明面面垂直，关键是把握住面面垂直的判定定理，在其中一个平面内找出另一个平面的垂线即可，而在找线面垂直时，需要把握住线面垂直的判定定理的内容，注意做好空间中的垂直转化工作，对于第二问，注意在求棱锥的体积时，注意把握住有关求体积的量是多少，底面积和高弄清楚后就没有问题.

试题解析：

（Ⅰ）证明：

在中,

在中，,

.3分

平面平面，且平面平面

平面,

平面，平面平面.6分

（Ⅱ）解：

过做,

平面平面平面且平面平面

平面,

四棱锥的高.8分

10分

则.12分

考点：

面面垂直的判定，棱锥的体积.

5．（Ⅰ）参考解析；（Ⅱ）参考解析；（Ⅲ）

【解析】

试题分析：

（Ⅰ）要证线面垂直等价转化为线线垂直，由圆周角所对的弦为直径即可得AF与BF垂直，再根据面面垂直的性质即可得CB与AF垂直.由此即可得到结论.

（Ⅱ）线面平行等价转化为线线平行，通过做DF的中点即可得到一个平行四边形，由此即可得到线线平行，即可得到结论.

（Ⅲ）根据四棱锥的体积公式，以及三棱锥的体积公式，其中有些公共的线段，由此即可求出两个体积的比值.

试题解析：

（Ⅰ）证明：

∵平面ABCD⊥平面ABEF，CB⊥AB，平面ABCD∩平面ABEF=AB，

∴CB⊥平面ABEF，∵AF平面ABEF，∴AF⊥CB，

又∵AB为圆O的直径，∴AF⊥BF，∴AF⊥平面CBF.

（Ⅱ）设DF的中点为N，则MN，又，

则，MNAO为平行四边形，

∴OM∥AN，又AN平面DAF，PM平面DAF，∴OM∥平面DAF.

（Ⅲ）过点F作FG⊥AB于G，∵平面ABCD⊥平面ABEF，

∴FG⊥平面ABCD，∴，

∵CB⊥平面ABEF，∴，

∴

考点：

1.线面垂直.2.线面平行.3.棱锥的体积公式.

6．（Ⅰ）详见解析（Ⅱ）详见解析（Ⅲ）

【解析】

试题分析：

Ⅰ）证明面面垂直，一般利用面面垂直判定定理，即从证明线面垂直出发：

因为面所以．又，所以面,所以平面面.（Ⅱ）证明线面平行，一般利用线面平行判定定理，即从证明线线平行出发，这一般可利用平面几何知识得以证明：

设，则易得四边形为平行四边形，所以//.所以//面（Ⅲ）求棱锥体积，关键在于确定其高。

可以利用等体积法将其转化为可确定高的棱锥：

试题解析：

（Ⅰ）证明:

因为为正方体，

所以面；

因为面，所以．2分

又因为，，所以面

因为面,所以平面面.5分

（Ⅱ）连接,//，且，

E

F

A

B

C

D

B1

A1

D1

C1

设，

则//且,

所以//且，

所以四边形为平行四边形.所以//.9分

又因为，．

所以//面11分

（Ⅲ）14分

考点：

面面垂直判定定理，线面平行判定定理，棱锥体积

7．（Ⅰ）证明见解析；（Ⅱ）

【解析】

试题分析：

（Ⅰ）将证明线面平行转化为线线平行，通过做辅助线可证明出//，线面平行的判定定理可证出平面；（Ⅱ）如图所示作辅助线，通过题意可先分将问题转化为求，由面面垂直的性质定理得平面，进而平面，得到平面，故，进而确定，再由

试题解析：

（Ⅰ）如图，连接，设，又点是的中点，

则在中，中位线//，