 数学分析教学大纲.docx
数学分析教学大纲.docx
- 文档编号:2241833
- 上传时间:2022-10-28
- 格式:DOCX
- 页数:20
- 大小:29.56KB
数学分析教学大纲.docx
《数学分析教学大纲.docx》由会员分享,可在线阅读,更多相关《数学分析教学大纲.docx(20页珍藏版)》请在冰豆网上搜索。
数学分析教学大纲
一、总则
本课程是数学专业最主要的专业必修课,它的任务是使学生获得极限论、一元函数微积分学、无穷级数与多元函数微积分学等方面的系统知识:
本课程是进一步学习复变函数论、微分方程、微分几何、概率论与数理统计、实变函数论、泛函分析等后继课程的阶梯,也为深入理解中学数学打下必要的基础:
通过本课程的讲授与作业应使学生:
1、对极限思想有较深刻的认识,基本上掌握通过极限方法研究初等函数性质的技巧。
2、正确理解数学分析的基本概念;熟悉基础理论,基本上掌握数学分析中的论证方法,获得熟练的演算技能,并具备初步的应用能力。
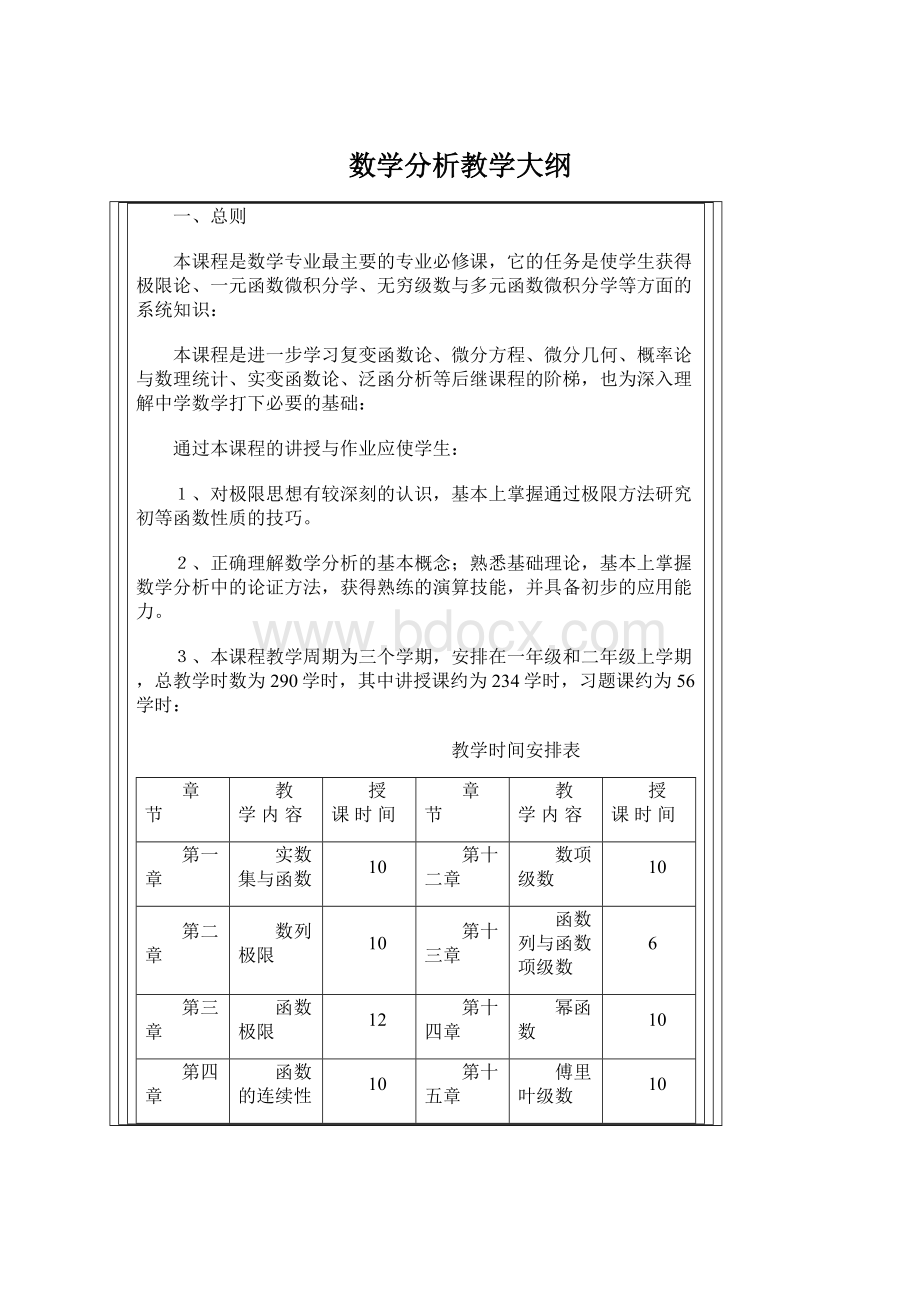
3、本课程教学周期为三个学期,安排在一年级和二年级上学期,总教学时数为290学时,其中讲授课约为234学时,习题课约为56学时:
教学时间安排表
章节
教学内容
授课时间
章节
教学内容
授课时间
第一章
实数集与函数
10
第十二章
数项级数
10
第二章
数列极限
10
第十三章
函数列与函数项级数
6
第三章
函数极限
12
第十四章
幂函数
10
第四章
函数的连续性
10
第十五章
傅里叶级数
10
第五章
导数与微分
12
第十六章
多元函数的极限与连续
8
第六章
微分中值定理及其应用
16
第十七章
多元函数微分学
14
第七章
实数的完备性
8
第十八章
隐函数定理及其应用
10
第八章
不定积分
8
第十九章
含参量积分
8
第九章
定积分
12
第二十章
曲线积分
8
第十章
定积分的应用
6
第二十一章
重积分
18
第十一章
反常积分
8
第二十二章
曲面积分
10
第二十三章
流形上微积分学初阶
10
二、具体教学安排
1、《数学分析
(一)》教学大纲
第一部分 总则
(1)本课程基本情况
课程编号:
11101101 课程类别:
专业必修 适用专业:
数学、信息和统计学
开课学期:
第一学期 总学时:
84 讲课学时:
78
习题课学时:
6 其 它:
学 分:
18
开课教研室:
函数论教研室;应用数学教研室;微分方程教研室。
(2)本课程的性质、目的和任务
本课程是数学与应用数学、信息与计算科学、、统计学专业的专业必修课中最重要的主干课程。
它的目的和任务是使学生获得极限论、一元函数微分学等方面的系统知识,并在学习知识的过程中,使学生在逻辑推理能力、计算能力、应用与创新能力等方面受到严格的专业训练,逐步培养学生良好的数学素养。
(3)本课程的基本要求
通过本课程的讲授与作业使学生
A、对极限思想有较深刻的认识,基本上掌握通过极限方法研究初等函数性质的技巧。
B、正确理解数学分析的基本概念,熟悉基础理论,基本上掌握数学分析中的论证方法,获得熟练的演算技能,并具备初步的应用能力。
(4)本课程与其他课程的联系和分工
本课程是进一步学习复变函数论、微分方程、微分几何、概率论、数理统计、数值分析、实变函数论、泛函分析等后继课程的阶梯,也为更深入理解中学数学打下必要的基础。
(5)课程的结构与学时安排
章序
标题
讲课学时
习题课学时
第一章
实数集与函数
10
0
第二章
数列极限
10
0
第三章
函数极限
12
2
第四章
函数的连续性
10
0
第五章
导数与微分
12
2
第六章
微分中值定理及其应用
16
0
第七章
实数的完备性
8
2
(6)使用教材与参考文献
使用教材:
华东师范大学数学系编《数学分析》(面向21世纪课程教材),北京:
高等教育出版社出版,第三版,2001年6月。
参考书目:
[1] 菲赫金哥尔茨著,叶彦谦等译,微积分学教程,北京:
人民教育出版社,1978。
[2] 陈傅璋等,数学分析,上海:
上海科学技术出版社,1962
[3] 欧阳光中等,数学分析,上海:
上海科学技术出版社,1982。
[4] 刘玉琏等,数学分析讲义(第三版),北京:
高等教育出版社,1992。
[5] 常庚哲等,数学分析教程,北京:
高等教育出版社,2003。
第二部分 各章节内容和学时分配
第一章 实数集与函数(10学时)
教学目标:
(1)掌握无限集、有界集、无界集、邻域的概念。
(2)理解实数的连续性、有序性、稠密性、阿基米德性质、实数对四则运算和正实数的开方运算的封闭性。
(3)掌握反函数的概念存在的必要条件与充分条件。
掌握初等绝对值不等式的证明技巧、能够证明简单函数的有界性、单调性、奇偶性与周期性、以及函数图象的平移、翻转、放缩叠加方法。
(4)逐步正确使用量词符号。
教法提示:
(1)重点:
绝对值不等式的解法与证明,函数的各种性态,有界集,确界原理的概念。
(2)难点:
确界原理。
教学内容:
(1)实数
实数及其性质、绝对值不等式。
(2)数集、确界原理
区间与邻域、有界集、确界原理。
(3)函数概念
函数的定义、函数的表示方法、函数的四则运算、复合函数、反函数、初等函数。
(4)具有某些特性的函数
有界函数、单调函数、奇函数与偶函数、周期函数。
第二章 数列极限(10学时)
教学目标:
1. 通过数列极限的教学将学生的认识领域从”有限”扩大到”无限”,逐步熟悉和理解极限方法。
2.深刻理解数列极限的ε---N定义,特别是ε的”任意”与”给定”的双重意义,以及对ε的依赖性,但同时也须明确N不是ε的函数。
3.理解无穷小数列的概念和它与极限间的关系,以及无穷大数列和无界数列的关系。
4.理解子序列的含义
5.掌握用ε---N定义证明有理式与简单无理式的极限。
6..深刻理解单调有界定理,迫敛性定理,子序列定理,逐步掌握灵活使用这些定理的技巧。
7.正确理解“ ” ,“ ”等不定型的含义及不确定性。
8.理解数列的“确界”与“极限”的关系。
教法提示:
1.重点:
数列极限的定义,数列极限的计算,迫敛性定理, 单调有界定理, 数列极限的柯西收敛准则,用子列刻划数列的收敛性。
2.难点:
数列极限的柯西收敛准则。
教学内容:
1.数列极限的概念
数列极限的定义,无穷小数列.
2.收敛数列的性质.
3.数列极限存在的条.
第三章 函数极限(12学时)
教学目标:
1.深刻理解“ ”与“ ”的定义,基本思想与几何意义,理解 在 处的极限与 在 处取值情况的无关性,以及 的过程中,取值的任意性。
2.掌握在“∞”、“+∞”、“-∞”处极限的定义与无穷大极限的定义,并能熟练地使用“ε-X”,“M-δ”等语言表述这些定义以及相应的逻辑非命题。
3.深刻理解有关无穷小量的一系列概念,无穷小量,等价无穷小,同阶无穷小……等。
4.深刻理解归结原理的含义,掌握其证明。
5.深刻理解函数极限的柯西收敛准则,掌握其证明。
6.熟练使用二个重要的极限计算某些不定型的极限。
7.对比数列极限的性质,明确函数极限的某些性质的局部性。
教法提示:
1.重点:
函数极限的定义,性质(唯一性,局部有界性,保号性),归结原则,柯西准则,两个重要极限。
2.难点:
函数极限的局部性质,柯西准则。
教学内容:
1.函数极限的概念
X趋于无穷大时函数的极限;X趋于某一定数时函数的极限。
2.函数极限的性质
3.函数极限存在的条件
4.两个重要极限
5.无穷小量与无穷大量,阶的比较
无穷小量,无穷小量阶的比较,无穷大量。
第四章 函数的连续性(10学时)
教学目标:
1.牢固掌握函数在一点处连续的定义的二种形式。
2.深刻理解单侧连续的定义及间断点的概念及其分类。
3.深刻理解“一致连续”的概念,理解“连续”是微观概念;“一致连续”是宏观概念;掌握闭区间上连续函数的基本性质。
4.掌握一般连续的逻辑非命是非命题及其在具体问题中的应用。
5.了解初等函数在其定义域内的连续性。
6.了解初等函数在其定义域内的连续性。
教法提示:
1.重点
2.难点
教学内容:
1.连续性的概念
函数在一点的连续性;间断点及其分类;区间上的连续函数.
2.连续函数的性质
连续函数的局部性质;闭区间上连续函数的基本性质;反函数的连续性;一致连续性.
3.初等函数的连续性
具有实指数的乘幂;指数函数的连续性;初等函数的连续性.
第五章 导数与微分(14学时)
教学目标:
1.深刻理解导数的定义与几何意义
2.深刻理解微分的定义与几何解释;以及一阶微分形式不变性的确切含义.
3.熟练掌握求导,求微分的方法.
4.掌握用单侧导数的定义求出函数在一些特殊点处的导数或着呢革命函数在该点的导数不存在的方法.
教学内容:
1.导数概念
导数的定义,导数的几何意义;导函数.
2.求导法则
导数的四则运算;反函数的导数;复合函数的导数;基本求导法则与公式.
3.微分
微分概念;微分的运算法则;近似计算与误差估计.
4.高阶导数与高阶微分
高阶导数;高阶微分;
5.微分方程所确定的函数的导数.
第六章 微分中值定理及其应用(18学时)
教学目标:
1.深刻理解拉格朗日定理及其推论,掌握定理的证明,它的几种形式。
2.理解费尔马定理,罗尔定理,柯西定理,泰勒定理的证明。
3.能用拉格朗日定理及其推论证明某些不等式掌握利用函数的泰勒展开式求一些函数的极限的方法。
4.熟悉掌握利用罗必达法则求各种不定型极限的方法。
5.掌握函数单调性与导数间的联系与几何意义;明确函数在某一点x。
处单调的含义。
掌握极限的要领与它的局部性质。
6.掌握函数凸凹的解析定义与几何意义。
掌握函数单调性,极值,凸凹性,拐点的判定方法。
了解凸函数的基本性质。
7.掌握利用导数证明不等式的基本方法。
掌握基本初等函数的特性作图方法。
教学内容:
1.中值定理
费尔马定理,中值定理
2.不定式极限
型不定式极限;〇╱〇型不定式极限;∞╱∞其他类型不定式极限;
3.泰勒公式
泰勒定理;带皮亚余项的泰勒公式;某些应用。
4. 函数的极值与最大(小)值。
极值判别法;最大值与最小值。
5. 函数的凸性与拐点
函数的凸性;拐点。
6.函数图象的讨论
渐进线;函数作图。
7.方程的近似解
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 数学分析 教学大纲
 冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 《巴黎圣母院》3000字读书心得范文.docx
《巴黎圣母院》3000字读书心得范文.docx
