数学算法初步.docx

数学算法初步.docx

《数学算法初步.docx》由会员分享，可在线阅读，更多相关《数学算法初步.docx（15页珍藏版）》请在冰豆网上搜索。

数学算法初步

15、算法初步

15．1算法的含义与流程图

【知识网络】

1．算法的含义，能用自然语言描述算法。

2．设计流程图表达解决问题的过程，了解算法和程序语言的区别；理解流程图的三种基本逻辑结构，会用流程图表示算法。

【典型例题】

[例1]

（1）下列关于算法的说法正确的是（）

A．某算法可以无止境地运算下去B．一个问题的算法步骤可以是可逆的

C．完成一件事情的算法有且只有一种D．设计算法要本着简单方便可操作的原则

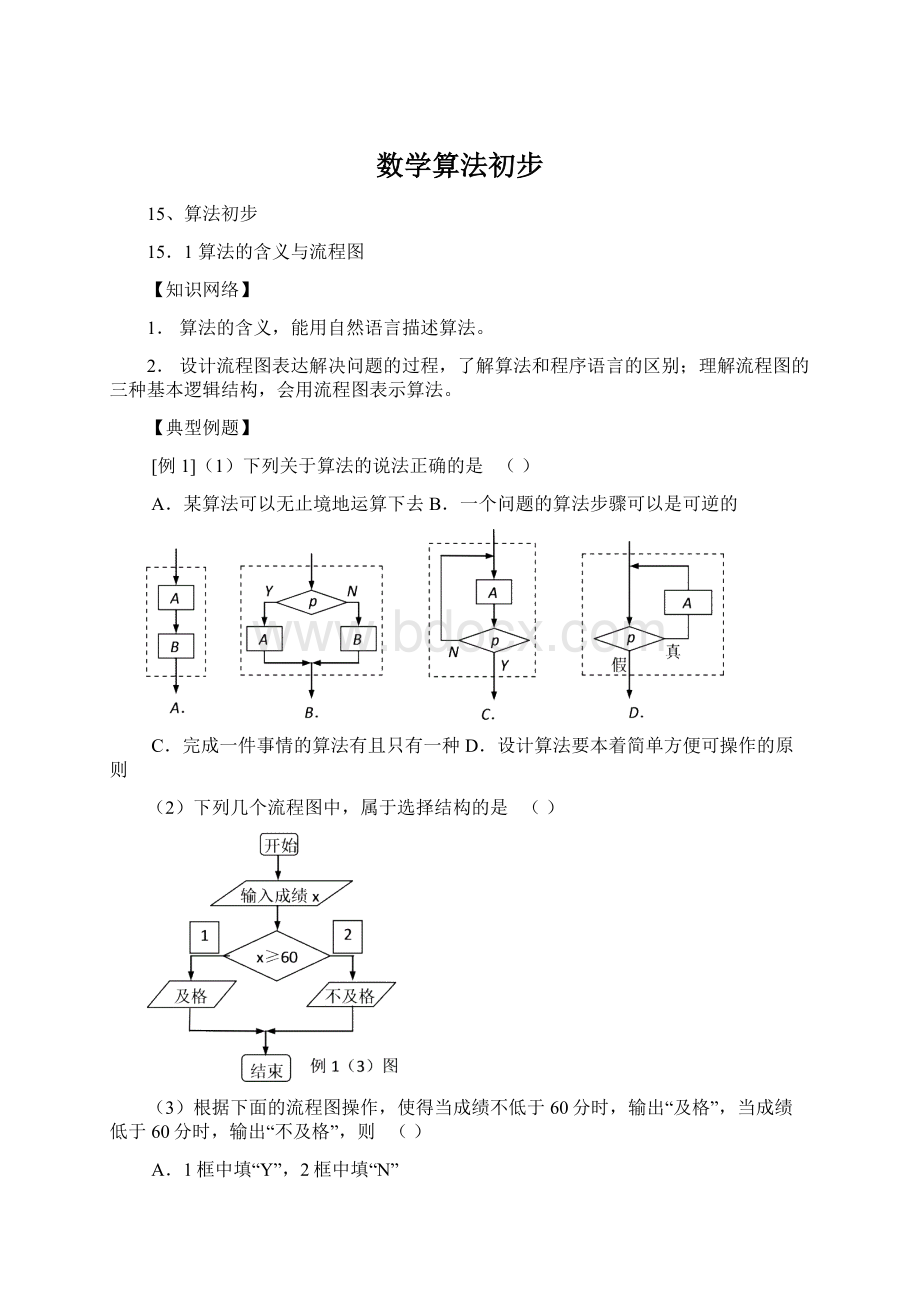
（2）下列几个流程图中，属于选择结构的是（）

（3）根据下面的流程图操作，使得当成绩不低于60分时，输出“及格”，当成绩低于60分时，输出“不及格”，则（）

A．1框中填“Y”，2框中填“N”

B．1框中填“N”，2框中填“Y”

C．1框中填“Y”，2框中可以不填

D．2框中填“N”，1框中可以不填

（4）流程图中的判断框，有1个入口和个出口．

（5）下列算法的功能是。

S1输入A，B；（A，B均为数据）

S2A←A+B，B←A-B，A←A-B；

S3输出A，B。

【例2】（找零钱问题）一个小孩买了价值少于1美元的糖，并将1美元的钱交给售货员．售货员希望用数目最少的硬币找给小孩．假设提供了数目不限的面值为25美分、10美分、5美分、及1美分的硬币．售货员分步骤组成要找的零钱数，每次加入一个硬币．选择硬币时所采用的规则如下：

①每一次选择应使零钱数尽量最大；②保证可行性（即：

所给的零钱等于要找的零钱数，所选择的硬币不应使零钱总数超过最终所需的数目．）

现假设买了34美分的糖．试根据以上材料写出找零钱的算法．

【例3】写出

（共7个2005）的值的一个算法，并画出流程图．

【例4】设计一个流程图，求满足10＜x2＜1000的所有正整数x的值．

【课内练习】

1．下面的四种叙述不能称为算法的是（）

A．广播操的广播操图解

B．歌曲的歌谱

C．做饭用米

D．做米饭需要刷锅、淘米、添水、加热这些步骤

2．早上从起床到出门需要洗脸刷牙（5min）、刷水壶（2min）、烧水（8min）、泡面（3min）、吃饭（10min）、听广播（8min）几个步骤.从下列选项中选出较好的一种算法（）

A．第一步洗脸刷牙、第二步刷水壶、第三步烧水、第四步泡面、第五步吃饭、第六步听广播

B．第一步刷水壶、第二步烧水同时洗脸刷牙、第三步泡面、第四步吃饭、第五步听广播

C．第一步刷水壶、第二步烧水同时洗脸刷牙、第三步泡面、第四步吃饭同时听广播

D．第一步吃饭同时听广播、第二步泡面、第三步烧水同时洗脸刷牙、第四步刷水壶

3．下列图形符号中，表示输入输出框的是（）

A．矩形框B．平行四边形框C．圆角矩形框D．菱形框

4．下面关于算法的基本结构叙述错误的为（）

A．任何算法都可以由三种基本结构通过组合与嵌套而表达出来

B．循环结构中包含着选择结构

C．选择结构中的两个分支，不能都是空的

D．有些循环结构可改为顺序结构

5．如图，输出的结果是．

6．如图，输出的．

7．已知函数f（x）=

，流程图表示的是给定x值，求其相应函数值的算法．请将该流程图补充完整．其中①处应填__________，②处应填__________．若输入x=3，则输出结果为．

8．画出计算1+3+5+…+99的算法流程图．

9．一个船工要送一匹狼、一只山羊和一棵白菜过河．每次除船工外，只能带一个乘客（狼、羊和白菜）渡河，并且狼和山羊不能单独在一起，山羊和白菜不能单独在一起，应如何渡河？

试画出算法的流程图．

10．某高中男子体育小组的50m赛跑成绩（单位：

s）为6.4，6.5，7.0，6.8，7.1，7.3，6.9，7.4，7.5，7.6，6.3，6.4，6.4，6.5，6.7，7.1，6.9，6.4，7.1，7.0．设计一个算法，从这些成绩中搜索出小于6.8s的成绩，并画出流程图．

15、算法初步

15．1算法的含义与流程图

A组

1．给出下列表述：

①利用海伦公式

计算边长分别为3，5，7的三角形的面积；

②从江苏南通到北京可以先乘汽车到上海再乘火车抵达；

③3y+2=x；

④求三点A（1，2），B（2，3），C（4，4）所在△ABC的面积可先算AB的长，再求AB的直线方程，求点C到直线AB的距离，最后利用S=

来进行计算．

其中是算法的有（）

A．1个B．2个C．3个D．4个

2．下列图形符号中，表示输入判断框的是（）

A．B．C．D．

3．下列算法的结果为（）

A．5，3B。

3，5C。

5，3，3，5D。

5，3，5，3

S1x←5，y←3；

S2x←x-y，y←y+x，x←y-x；

S3输出x，y。

4．买一个茶杯1.5元，现要写出计算买n个茶杯所需要的钱数的一个算法，则这个算法中必须要用到的一个算法表达式为．

5．如图，输出结果为。

6．所谓正整数p为素数是指：

p的所有约数只有1和p．例如35不是素数，因为35的约数除了1、35，还有5与7．29是素数，因为29的约数就只有1和29．

试设计一个能够判断一个任意正整数n（n＞1）是否为素数的算法．

7．某工厂2004年的生产总值为200万元，技术革新后预计以后每年的生产总值比上一年增加5%，问最早需要哪一年年生产总值超过300万元．写出计算的一个算法并画出相应的程序框图．

8．画出求13+23+…+1003值的流程图．

15、算法初步

15．1算法的含义与流程图

B组

1．在算法中，需要重复执行同一操作的结构称为（）

A．顺序结构B．循环结构C．选择结构D．分支结构

2．下列算法中含有选择结构的是（）

A．求点到直线的距离B．已知梯形两底及高求面积

C．解一元二次方程D．求两个数的积

3．下列所画流程图是已知直角三角形两条直角边a、b求斜边的算法，其中正确的是（）

4．图中是求50个数中的最大数并输出最大数的流程图．则①中的条件应为，②中的条件应为．

5．下列四个流程图，都是为计算22+42+62+…+1002而设计的．正确的流程图为；图3中，输出的结果为（只须给出算式表达式）；在错误的流程图中，不能执行到底的为．

6．给定任意两个整数，按从小到大的顺序排列，试画出它的算法流程图．

7．写出判断函数y=f（x）奇偶性的一个算法，并画出流程图．

8．试设计求

（n≥2）的值的算法的程序框图.

参考答案

15．1算法的含义与流程图

【典型例题】

[例1]

（1）D。

提示：

由算法的特点所确定。

（2）B．提示：

根据选择结构的意义．C、D选项属于循环结构．

（3）A．提示：

判断框的两个出口必须均有选择。

另及格满足x≥60，故选择“Yes”。

（4）2．提示：

判断框的两个出口分别选择“是”（Y）或“否”（N）。

（5）实现数据A，B的互换。

提示：

利用赋值语句的意义与题中算法的步骤进行分析。

【例2】第一步先计算100-34=66；

第二步判断66≥25：

是．

第三步找25美分；余额41；

第四步判断41≥25：

是．

第五步找25美分；余额16；

第六步判断16≥25．否．

第七步判断16≥10：

是．

第八步找10美分；余额6；

第九步判断6≥10：

否．

第十步判断6≥5：

是．

第十一步找5美分；余额1；

第十二步找1美分．找零钱算法结束．

【例3】S1

；

S2I←1；

S3

；

S4I←I+1；

S5如果I＞6，则输出m的值，转S6；否则，转S3；

S6结束．

【例4】见图所示。

【课内练习】

1．C。

提示：

算法必须要有步骤的，步骤必须明确的。

2．C。

提示：

要使算法尽量过程合理，用时最少。

3．B。

提示：

圆角矩形框表示开始或结束框；矩形框表示处理框；菱形框表示判断框。

4．C。

提示：

循环结构中必须包括选择结构，否则循环不能结束。

5．12。

提示：

m=2，p=7，m=12。

6．105。

提示：

T=1，I=1，T=1，I=3，不满足条件；T=3，I=5，不满足条件；T=15，I=7，不满足条件；T=105，I=9，满足条件。

输出T。

7．①:

x≤3；②y←-3x2；5．提示：

根据给出函数的解析式分析可填出。

8．见答图。

9．见答图。

10．S1i←1；

S2输入Ni，Gi；

S3如果Gi＜6.8，则输出Ni，Gi，并执行S4，否则，也执行S4；

S4i←i+1；

S5如果i≤20，则返回S2，否则结束．

图见答图所示．

15、算法初步

15．1算法的含义与流程图

A组

1．C。

提示：

①②④是算法。

2．C。

提示：

判断框应是一个菱形。

3．B。

提示：

算法是将A，B的值互相交换。

4．

（n∈N*）。

5．9。

提示：

逐个取值验证。

6．第一步给出任意一个正整数n（n＞1）；

第二步若n=2，则输出“2是素数”，判断结束；

第三步m←1{把1赋给变量m}

第四步m←m+1{把m+1的值赋给m}

第五步如果m≥n，则输出“n是素数”，判断结束；

第六步判断m能否整除n．

①如果能整除，则输出“n不是素数”，判断结束；

②如果不能整除，则转第四步．

7．S1n←0，a←200，r←0.05；

S2T←ar（计算年增量）；

S3a←a+T（计算年产值）；

S4如果a≤300，那么n←n+1，重复执行S2；

S5N←2004+n；

S6输出N．

流程图见如图所示．

8．见答图8-1或答图8-2。

B组

1．B。

提示：

按循环结构的意义可得。

2．C。

提示：

解一元二次方程时，必须首先判断根的“判别式”的与0的大小间的关系，这便是条件判断，故解一元二次方程时须用选择结构。

3．A。

提示：

C、D选项中的有些框图选用不正确；B图中的输入变量的值应在公式给出之前完成。

4．①：

b＜ai；②i＞50．

5．正确的图为图4；结果为22+42+62+…+982；错误图中不能执行到底的为图2．

6．见答图6。

7．算法如下：

第一步求函数y=f（x）的定义域D；

第二步若D关于原点对称，则转第三步，否则输出“f（x）为非奇非偶函数”，结束；

第三步求f（-x）；

第四步判断f（-x）=f（x）？

成立，输出“f（x）为偶函数”，结束；

否则，转第五步；

第五步判断f（-x）=-f（x）？

成立，输出“f（x）为奇函数”，结束；

否则，输出“f（x）为非奇非偶函数”，结束．

流程图如答图7所示．

8．算法为：

S1输入n；

S2m←sqr（2006）；

S3I←2；

S4m←sqr（2006m）；

S4I←I+1；

S5如果I＞n，则输出m的值，转S6；否则，转S4；

S6结束．

流程图见答图8-1或答图8-2．

本资料来源于《七彩教育网》