二元一次方程组应用题复习.docx

二元一次方程组应用题复习.docx

《二元一次方程组应用题复习.docx》由会员分享，可在线阅读，更多相关《二元一次方程组应用题复习.docx（6页珍藏版）》请在冰豆网上搜索。

慧智教育中小学个性化课外辅导

课题二元一次方程组应用题

课时单编号：

教师姓名

班主任姓名

教学主管

日期

时间段

本次课时数

累计课时数

教学目标

探究二元一次方程组解决实际问题

进一步提高分析问题中的等量关系、设未知数、列方程组、解方程组的能力。

教学重点

二元一次方程组解决实际问题

教学难点

分析问题中的等量关系

教学方法

启发式、讲练结合、归纳总结

素材来源

教辅资料

教学步骤

教学内容

知识与方法

知识点梳理

一、知识点梳理：

1、列方程组解应用题的基本思想：

列方程组解应用题是把“未知”转化为“已知”的重要方法，它的关键是把已知量和未知量联系起来，找出题目中的相等关系.

2、利用二元一次方程组解决实际问题的步骤：

（1）审题:

弄清题意及题目中的数量关系；

（2）设未知数:

可直接设元，也可间接设元；

　（3）找出题目中的等量关系；

（4）列出方程组:

根据题目中表示全部含义的等量关系列出方程，并组成方程组；

（5）解所列的方程组，并检验解的正确性；

（6）写出答案.

题型归类

二、题型归类

类型一：

行程问题

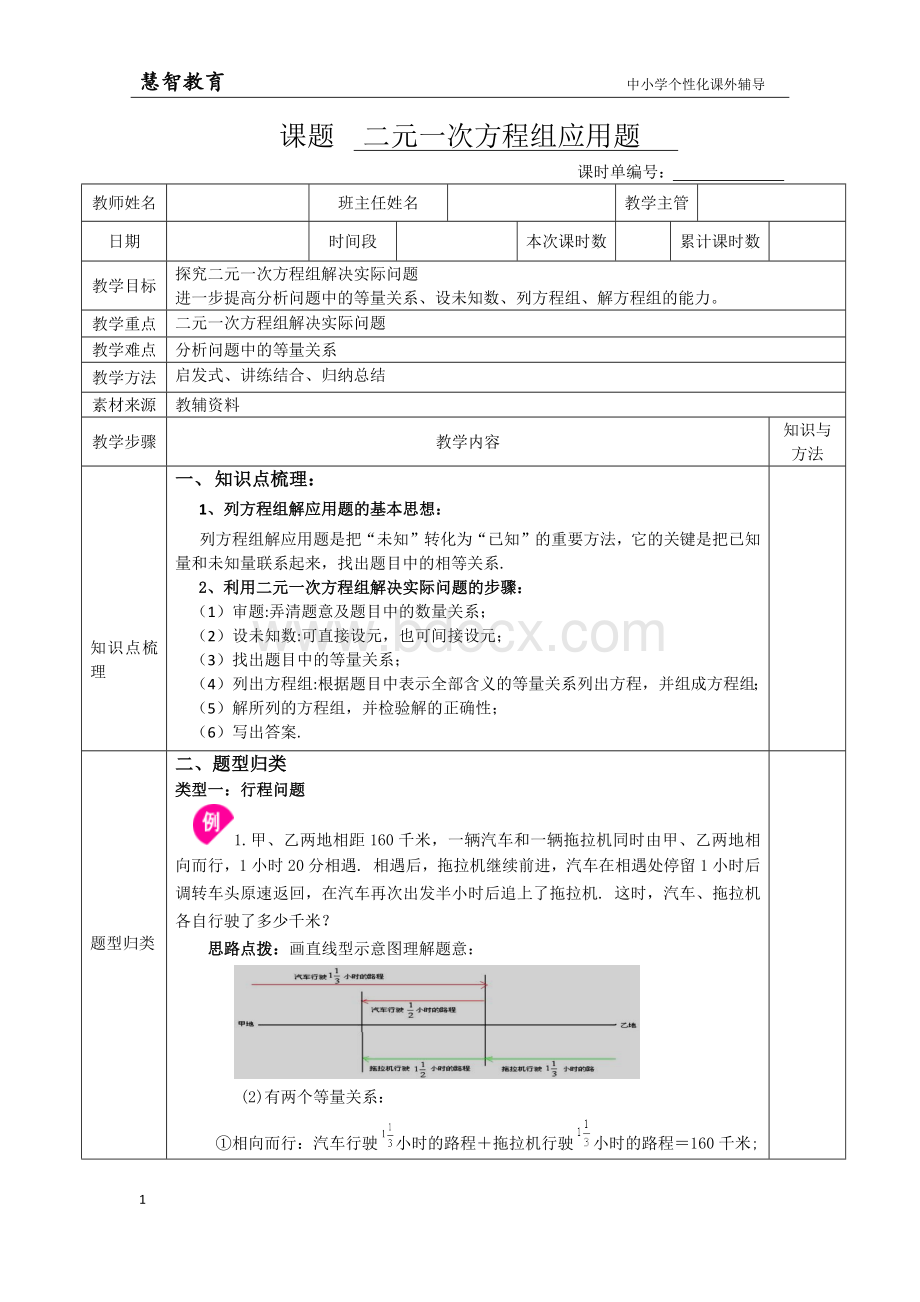
　1.甲、乙两地相距160千米，一辆汽车和一辆拖拉机同时由甲、乙两地相向而行，1小时20分相遇.相遇后，拖拉机继续前进，汽车在相遇处停留1小时后调转车头原速返回，在汽车再次出发半小时后追上了拖拉机.这时，汽车、拖拉机各自行驶了多少千米？

　　思路点拨：

画直线型示意图理解题意：

（2）有两个等量关系：

　　①相向而行：

汽车行驶小时的路程＋拖拉机行驶小时的路程＝160千米;

　　　②同向而行：

汽车行驶小时的路程＝拖拉机行驶小时的路程.

　　解：

设汽车的速度为每小时行千米，拖拉机的速度为每小时千米.

　　　　根据题意，列方程组　　　　解这个方程组，得:

　　　　.

　　答：

汽车行驶了165千米，拖拉机行驶了85千米.

总结升华：

列方程组解应用题，首先要设未知数，多数题目可以直接设未知数，但并不是千篇一律的，问什么就设什么。

有时候需要设间接未知数，有时候需要设辅助未知数。

练习：

甲、乙两人相距36千米，相向而行，如果甲比乙先走2小时，那么他们在乙出发2.5小时后相遇；如果乙比甲先走2小时，那么他们在甲出发3小时后相遇，甲、乙两人每小时各走多少千米？

类型二：

工程问题

　2.一家商店要进行装修，若请甲、乙两个装修组同时施工，8天可以完成，需付两组费用共3520元；若先请甲组单独做6天，再请乙组单独做12天可完成，需付两组费用共3480元，问：

（1）甲、乙两组工作一天，商店应各付多少元？

（2）已知甲组单独做需12天完成，乙组单独做需24天完成，单独请哪组，商店所付费用最少？

　　解：

（1）设甲组单独做一天商店应付x元，乙组单独做一天商店应付y元，依题意得：

　　　　　　　　　　解得

　　　　答：

甲组单独做一天商店应付300元，乙组单独做一天商店应付140元。

（2）单独请甲组做，需付款300×12＝3600元，单独请乙组做，需付款24×140＝3360元，故请乙组单独做费用最少。

练习：

小明家准备装修一套新住房，若甲、乙两个装饰公司合作6周完成需工钱5.2万元；若甲公司单独做4周后，剩下的由乙公司来做，还需9周完成，需工钱4.8万元.若只选一个公司单独完成，从节约开支的角度考虑，小明家应选甲公司还是乙公司？

请你说明理由.

类型三：

商品销售利润问题

　　3.有甲、乙两件商品，甲商品的利润率为5%,乙商品的利润率为4%,共可获利46元。

价格调整后，甲商品的利润率为4%，乙商品的利润率为5%，共可获利44元，则两件商品的进价分别是多少元？

　　思路点拨：

做此题的关键要知道：

利润＝进价×利润率

　　解：

甲商品的进价为x元，乙商品的进价为y元，由题意得：

　　　　，解得：

　　答：

两件商品的进价分别为600元和400元。

练习：

某商场用36万元购进A、B两种商品，销售完后共获利6万元，其进价和售价如下表：

A

B

进价（元/件）

1200

1000

售价（元/件）

1380

1200

求该商场购进A、B两种商品各多少件；（注：

获利=售价—进价）

类型四：

银行储蓄问题

　4．小明的妈妈为了准备小明一年后上高中的费用，现在以两种方式在银行共存了2000元钱，一种是年利率为2.25％的教育储蓄，另一种是年利率为2.25％的一年定期存款，一年后可取出2042.75元，问这两种储蓄各存了多少钱？

（利息所得税＝利息金额×20%，教育储蓄没有利息所得税）

　　思路点拨：

设教育储蓄存了x元，一年定期存了y元，我们可以根据题意可列出表格：

　　解：

设存一年教育储蓄的钱为x元，存一年定期存款的钱为y元，则列方程：

　　　　，解得：

　　答：

存教育储蓄的钱为1500元，存一年定期的钱为500元.

练习：

李明以两种形式分别储蓄了2000元和1000元，一年后全部取出，扣除利息所得税可得利息43.92元.已知两种储蓄年利率的和为3.24%，问这两种储蓄的年利率各是百分之几？

（注：

公民应缴利息所得税=利息金额×20%）

类型五：

生产中的配套问题

　　5．某服装厂生产一批某种款式的秋装，已知每2米的某种布料可做上衣的衣身3个或衣袖5只.现计划用132米这种布料生产这批秋装（不考虑布料的损耗），应分别用多少布料才能使做的衣身和衣袖恰好配套？

　　　　解：

设用x米布料做衣身，用y米布料做衣袖才能使衣身和衣袖恰好配套，根据题意，得：

　　答：

用60米布料做衣身，用72米布料做衣袖才能使做的衣身和衣袖恰好配套.

练习：

某工厂有工人60人，生产某种由一个螺栓套两个螺母的配套产品，每人每天生产螺栓14个或螺母20个，应分配多少人生产螺栓，多少人生产螺母，才能使生产出的螺栓和螺母刚好配套。

类型六：

利润率问题

6.某工厂去年的利润（总产值—总支出）为200万元，今年总产值比去年增加了20%，总支出比去年减少了10%，今年的利润为780万元，去年的总产值、总支出各是多少万元？

　　思路点拨：

设去年的总产值为x万元，总支出为y万元，则有

总产值（万元）

总支出（万元）

利润（万元）

去年

x

y

200

今年

120%x

90%y

780

　　解：

设去年的总产值为x万元，总支出为y万元，根据题意得：

　　　　，解之得：

　　答：

去年的总产值为2000万元，总支出为1800万元

　练习：

某城市现有人口42万，估计一年后城镇人口增加0.8%，农村人口增加1.1%，这样全市人口增加1%，求这个城市的城镇人口与农村人口。

类型七：

浓度问题

　7．现有两种酒精溶液，甲种酒精溶液的酒精与水的比是3∶7，乙种酒精溶液的酒精与水的比是4∶1，今要得到酒精与水的比为3∶2的酒精溶液50kg，问甲、乙两种酒精溶液应各取多少？

　　思路点拨：

本题欲求两个未知量，可直接设出两个未知数，然后列出二元一次方程组解决，题中有以下几个相等关系：

（1）甲种酒精溶液与乙种酒精溶液的质量之和＝50；

（2）混合前两种溶液所含纯酒精质量之和＝混合后的溶液所含纯酒精的质量；

　　解：

设甲、乙两种酒精溶液分别取xkg,ykg.依题意得：

　　　　　　，

　　　　　　　答：

甲取20kg，乙取30kg

练习：

要配浓度是45%的盐水12千克，现有10%的盐水与85%的盐水，这两种盐水各需多少？

类型八：

优化方案问题：

8．某地生产一种绿色蔬菜，若在市场上直接销售，每吨利润为1000元；经粗加工后销售，每吨利润可达4500元；经精加工后销售，每吨利润涨至7500元.当地一家农工商公司收获这种蔬菜140吨，该公司加工厂的生产能力是：

如果对蔬菜进行粗加工，每天可以加工16吨；如果进行细加工，每天可加工6吨.但两种加工方式不能同时进行.受季节条件的限制，公司必须在15天之内将这批蔬菜全部销售或加工完毕，为此公司研制了三种加工方案

　　方案一：

将蔬菜全部进行粗加工；

　　方案二：

尽可能多的对蔬菜进行精加工，没来得及加工的蔬菜在市场上直接销售；

　　方案三：

将部分蔬菜进行精加工，其余蔬菜进行粗加工，并恰好在15天完成

　　你认为选择哪种方案获利最多？

为什么？

　　　　解：

方案一获利为：

4500×140=630000（元）.

方案二获利为：

7500×（6×15）+1000×（140－6×15）=675000+50000=725000（元）.

　　　　方案三获利如下：

　　　　设将吨蔬菜进行精加工，吨蔬菜进行粗加工，则根据题意，得：

　　　，解得：

所以方案三获利为：

7500×60+4500×80=810000（元）.

　　因为630000＜725000＜810000，所以选择方案三获利最多

答：

方案三获利最多，最多为810000元。

练习：

某商场计划拨款9万元从厂家购进50台电视机，已知厂家生产三种不同型号的电视机，出厂价分别为：

甲种每台1500元，乙种每台2100元，丙种每台2500元。

（1）若商场同时购进其中两种不同型号的电视机50台，用去9万元，请你研究一下商场的进货方案；

（2）若商场销售一台甲、乙、丙电视机分别可获利150元、200元、250元，在以上的方案中，为使获利最多，你选择哪种进货方案？

类型九：

几何问题

　　9.如图，用8块相同的长方形地砖拼成一个长方形，每块长方形地砖的长和宽分别是多少？

　　解：

设长方形地砖的长xcm,宽ycm，由题意得：

　　　，

　　答：

每块长方形地砖的长为45cm、宽为15cm。

练习：

用长48厘米的铁丝弯成一个矩形，若将此矩形的长边剪掉3厘米，补到较短边上去，则得到一个正方形，求正方形的面积比矩形面积大多少？

课后作业

四、课后作业

1、两地相距280千米，一艘船在其间航行，顺流用14小时，逆流用20小时，求船在静水中的速度和水流速度。

2、小敏的爸爸为了给她筹备上高中的费用，在银行同时用两种方式共存了4000元钱.第一种，一年期整存整取，共反复存了3次，每次存款数都相同，这种存款银行利率为年息2.25%；第二种，三年期整存整取，这种存款银行年利率为2.70%.三年后同时取出共得利息303.75元，问小敏的爸爸两种存款各存入了多少元？

（不计利息税）

3、现有190张铁皮做盒子，每张铁皮做8个盒身或22个盒底，一个盒身与两个盒底配成一个完整盒子，问用多少张铁皮制盒身，多少张铁皮制盒底，可以正好制成一批完整的盒子？

4、一种35%的新农药，如稀释到1.75%时，治虫最有效。

用多少千克浓度为35%的农药加水多少千克，才能配成1.75%的农药800千克？

6