 江苏省七年级下几何提优练习精选题.docx
江苏省七年级下几何提优练习精选题.docx
- 文档编号:1724798
- 上传时间:2022-10-23
- 格式:DOCX
- 页数:21
- 大小:1.62MB
江苏省七年级下几何提优练习精选题.docx
《江苏省七年级下几何提优练习精选题.docx》由会员分享,可在线阅读,更多相关《江苏省七年级下几何提优练习精选题.docx(21页珍藏版)》请在冰豆网上搜索。
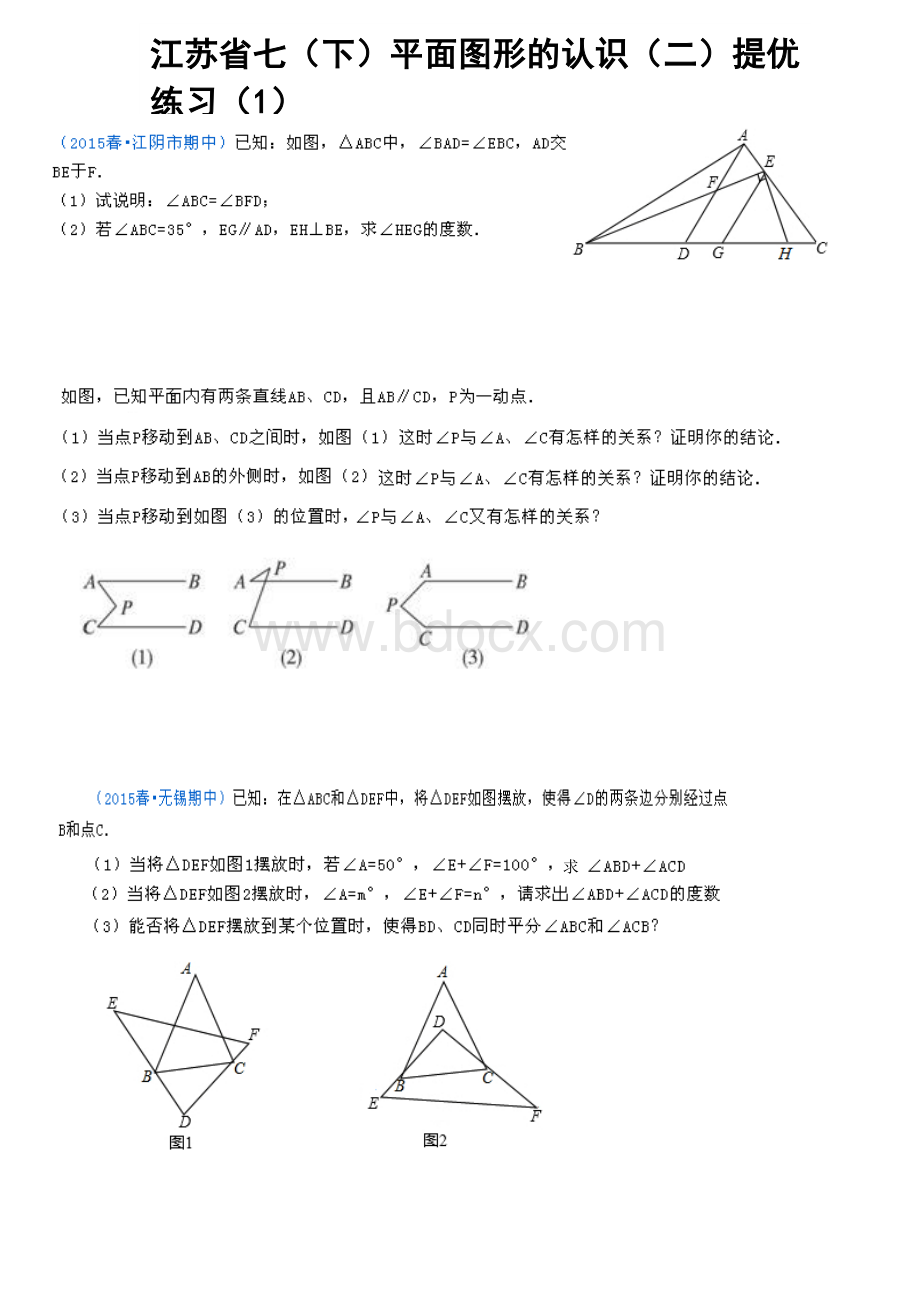
江苏省七(下)平面图形的认识
(二)提优练习
(1)
求
在△ABC中,∠C=90°,点D、E分别是边Ac、BC上的点,点P是一动点,连接PD、PE,∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)如图1所示,若点P在线段AB上,且∠α=40°,则∠1+∠2= °;
(2)如图2所示,若点P在边AB上运动,则∠α、∠1、∠2之间的关系为有何数量关系;猜想结论并说明理由;
(3)如图3所示,若点P运动到边AB的延长线上,则∠α、∠1、∠2之间有何数量关系?
猜想结论并说明理由.
(1)如图①,△ABC中,点D、E在边BC上,AD平分∠BAC,AE⊥BC,∠B=35°,∠C=65°,求∠DAE的度数;
(2)如图②,若把
(1)中的条件“AE⊥BC”变成“F为DA延长线上一点,FE⊥BC”,其它条件不变,求∠DFE的度数;
(3)若把
(1)中的条件“AE⊥BC”变成“F为AD延长线上一点,FE⊥BC”,其它条件不变,请画出相应的图形,并求出∠DFE的度数;
(4)结合上述三个问题的解决过程,你能得到什么结论?
已知:
∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则①∠ABO的度数是;20°;;②如图2,当∠BAD=∠ABD时,试求x的值(要说明理由)120°;60°
(2)如图3,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?
若存在,直接写出x的值;若不存在,说明理由.(自己画图)
聪明的小宸同学在学习“三角形的外角等于与它不相邻的两个内角之和”后,采用类比的方法,研究四边形不相邻的两个外角与不相邻的两个内角的关系.
(1)如图①,猜想并说明∠1+∠2与∠A、∠C的数量关系;
(2)图①不妨称为“枪头图”.试直接利用上述结论,解决下面的三个问题:
问题一:
如图②,将△ABC纸片沿DE折叠,使点彳落在四边形BCDE内点A’的位置,
试直接写出∠1+∠2与∠A之间的数量关系:
;
问题二:
如图③,在△ABC中,∠ABC与∠ACB的外角平分线交于点D,若∠A=40°,求∠O的度数;
问题三:
将图③中边BC改为折线BDC?
得图④,BO、CO是∠ABD与∠ACD的外角平分线.
试探究:
∠A、∠D与∠O这三个角的数量关系.
如图①,AD是△ABC的中线,△ABD与△ACD的面积有怎样的数量关系?
为什么?
(2)若三角形的面积记为S,例如:
△ABC的面积记为S△ABC,如图②,已知S△ABC=1,△ABC的中线AD、CE相交于点O,求四边形BDOE的面积.
小华利用
(1)的结论,解决了上述问题,解法如下:
连接BO,设S△BEO=x,S△BDO=y,
由
(1)结论可得:
S,
S△BCO=2S△BDO=2y,
S△BAO=2S△BEO=2x.
则有,即.
所以.
请仿照上面的方法,解决下列问题:
①如图③,已知S△ABC=1,D、E是BC边上的三等分点,F、G是AB边上的三等分点,AD、CF交于点O,求四边形BDOF的面积.
②如图④,已知S△ABC=1,D、E、F是BC边上的四等分点,G、H、I是AB边上的四等分点,AD、CG交于点O,则四边形BDOG的面积为 .
平面内的两条直线有相交和平行两种位置关系
(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB、CD内部,如图b,以上结论是否成立?
若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?
请证明你的结论;
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?
(不需证明)
(3)根据
(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.
如图1,两个不全等的等腰直角三角形OAB和OCD叠放在一起,并且有公共的直角顶点O。
(1)在图1中,你发现线段AC、BD的数量关系是 ______________;直线AC、BD相交成角的度数是_____________.
(2)将图1的⊿OAB绕点O顺时针旋转90°角,在图2中画出旋转后的⊿OAB。
(3)将图1中的⊿OAB绕点O顺时针旋转一个锐角,连接AC、BD得到图3,这时
(1)中的两个结论是否成立?
作出判断并说明理由。
若⊿OAB绕点O继续旋转更大的角时,结论仍然成立吗?
作出判断,不必说明理由。
如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.
(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?
若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?
若存在,请求出
∠OBA度数;若不存在,说明理由.
操作与实践
(1)如图1,已知△ABC,过点A画一条平分三角形面积的直线;
(2)如图2,已知l1∥l2,点E,F在l1上,点G,H在l2上,试说明△EGO与△FHO的面积相等;
(3)如图3,点M在△ABC的边上,过点M画一条平分三角形面积的直线.
在△ABC中,∠A=40o。
(1)如图
(1)BO、CO是△ABC的内角角平分线,且相交于点O,求∠BOC的度数
(2)如图
(2)若BO、CO是△ABC的外角角平分线,且相交于点O,求∠BOC的度数;
(3)如图(3)若BO、CO分别是△ABC的一内角角平分线和一外角角平分线,且相交于点O,求∠BOC的度数;
(4)根据上述三问的结果,当∠A=no时,分别可以得出∠BOC与∠A有怎样的数量关系.
提炼1:
三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:
如图,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
提炼2:
若将△ADC改为任意四边形ABCD呢?
已知:
如图,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
提炼3:
若将上题中的四边形ABCD改为六边形ABCDEF呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:
________________.
(1)如图1的图形我们把它称为“8字形”,请说明;
(2)阅读下面的内容,并解决后面的问题:
如图2,AP、CP分别平分∠BAD.∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数;
解:
∵AP、CP分别平分∠BAD.∠BCD
∴∠1=∠2,∠3=∠4
由
(1)的结论得:
①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P=(∠B+∠D)=26°.
①如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想的度数,并说明理由.
②在图4中,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
③在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 江苏省 年级 几何 练习 精选
 冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 12处方点评管理规范实施细则_精品文档.doc
12处方点评管理规范实施细则_精品文档.doc
 17种抗癌药纳入国家基本医疗保险工伤保险和生育保险药品目录_精品文档.xls
17种抗癌药纳入国家基本医疗保险工伤保险和生育保险药品目录_精品文档.xls
